Factorización: Factor común

Factorizar una expresión algebraica consiste en escribirla como un producto.

Factor común monomio

Un factor común monomio, es el factor que está presente en cada término del polinomio. En el caso de los coeficientes numéricos el factor común es el mayor divisor posible entre ellos y el factor común literal está conformado por el o los elementos de la parte literal presentes en todos los términos con el menor exponente.

Para factorizar el polinomio, se escribe el factor común monomio multiplicado por el polinomio resultante de dividir cada término del polinomio original entre el factor común monomio.

Ejemplos

Factorizar

$\1. \quad 12x+18y-24$

El factor común numérico es el 6, puesto que 6 es el mayor divisor entre 12, 18 y 24 (nótese que 3 es divisor de 12, 18 y 24, pero el que necesitamos es el mayor posible), luego no tenemos factor común literal ya que no hay elementos en cada factor literal que se repita en todos los términos, por lo tanto, la factorización es:

$\2. \quad 5a^2-15ab-10ac$

El factor común entre los coeficientes es 5 (mayor divisor de 5, 10 y 15), y entre los factores literales es a (factor literal que se repite en todos los términos con el menor exponente), por lo tanto

$\3. \quad 6x^2y-30xy^2+12x^2y^2$

El factor común es “6xy “porque 6 es el mayor divisor y los términos con el menor exponente en cada caso son xy, elementos del factor literal presentes en todos.

Ejercicios

Factorizar:

Factor común polinomio

Es el polinomio que aparece en cada término de la expresión, ahora el factor común resulta ser un polinomio.

Ejemplos

Factorizar

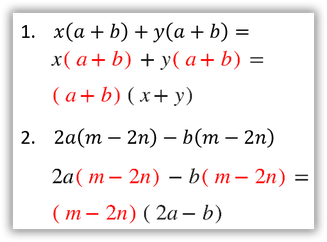
Ejercicios

Factorizar

Factor común agrupando términos

Se trata de agrupar términos de manera que entre cada grupo podamos obtener un factor común y de esta forma si es posible obtener a su vez un factor común polinomio.

Ejemplo

Ejercicios

Factorizar