Lógica

CONECTIVAS

Al realizar razonamientos empleamos sentencias que están conectadas entre sí por conectivas lingüísticas. La lógica proposicional se ocupa del estudio de las conectivas lingüísticas entre proposiciones. Una proposición es una sentencia que puede ser verdadera, circunstancia que indicaremos asociándola el valor de verdad V , o falsa, en cuyo caso le asociaremos el valor de verdad F. Nuestro principal interés en relación con la lógica proposicional es dejar establecido el papel que juegan las conectivas lingüísticas y sus conectivos lógicos asociados en relación con los conceptos de verdad y demostración.

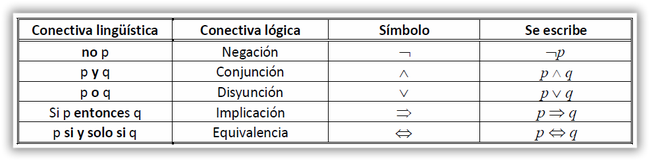
Las conectivas lingüísticas permiten construir proposiciones compuestas a partir de otras más simples. Así, si los símbolos p y q representan proposiciones genéricas, las conectivas lingüísticas más empleadas son las que aparecen en la siguiente tabla:

NEGACIÓN

El significado de la conectiva lógica negación, reside en que la proposición ¬p es verdadera en el caso de que p sea falsa y recíprocamente que ¬p es falsa cuando p es verdadera. Recogemos el significado del conectivo ¬ en la siguiente tabla de verdad:

Del mismo modo podemos recoger el significado del resto de las conectivas.

CONJUNCIÓN

La sentencia $p\land q$ es verdadera sólo cuando p y q son verdaderas simultáneamente. La tabla de verdad correspondiente a esta conectiva será, pues:

DISYUNCIÓN

La sentencia $p\lor q$, que se lee p ó q; debe entenderse en su acepción más amplia, es decir, p ó q o ambos; con lo que $p\lor q$ será verdadera en el caso de que p sea verdadera, q sea verdadera o ambas sean verdaderas simultáneamente:

IMPLICACIÓN

Para establecer el significado de la sentencia $p\Rightarrow q$ , que se lee si p entonces q o también p implica q; debemos tener presente que en lenguaje natural la sentencia p implica q encierra una relación de causalidad, causalidad que no siempre aparece al utilizar este conectivo en el ámbito formal. Se pretende que el valor V o F de la sentencia $p\Rightarrow q$  dependa por completo de los valores de verdad de p y q, con independencia de que exista o no alguna relación de causalidad con sentido entre p y q. En lenguaje matemático, p implica q quiere decir que, si p es verdadera, necesaria- mente q es verdadera, o lo que es lo mismo, que es imposible que q sea falsa y p verdadera: Esto es, si el valor de verdad de p es V y el de q es F, el valor de verdad de $p\Rightarrow q$  es F; para el resto de posibles valores de p y q la sentencia será verdadera. Considérese el ejemplo siguiente:

Sea la proposición: Si quemo madera, hay humo en el ambiente, que representaremos por   $p\Rightarrow q$. Entendemos que esta sentencia es verdadera, puesto que en nuestra experiencia no encontramos una situación en la que una madera esté ardiendo y no produzca humo. Sin embargo, la sentencia es verdadera independientemente de que se tenga madera a mano y no haya humo en el ambiente, de que no estemos quemando madera y haya humo debido a que estamos que- mando papel, o incluso de que efectivamente estemos quemando madera y se esté llenando el ambiente de humo. En otras palabras $p\Rightarrow q$  sigue siendo verdadera aun en el caso en el que p sea falsa (no estemos quemando madera) y q sea falsa (no hay humo en el ambiente), p sea falsa y q sea verdadera o incluso que p sea verdadera y q sea verdadera. El significado de este conectivo lógico queda pues del siguiente modo: 

Es importante destacar que de la tabla anterior se sigue que para demostrar que la sentencia $p\Rightarrow q$  es verdadera, basta con estudiar el caso en el que p es verdadera, puesto que, si p es falsa, la sentencia $p\Rightarrow q$  es verdadera.

 A las sentencias p y q las denominaremos, respectivamente, antecedente y consecuente de la proposición  $p\Rightarrow q$ 

La sentencia $q\Rightarrow p$  es denominada sentencia recíproca de la sentencia $p\Rightarrow q$  ; y la sentencia: $q\Rightarrow p$  sentencia contrarrecíproca de la sentencia  $p\Rightarrow q$

EQUIVALENCIA

La proposición $p\Longleftrightarrow q$ , que se lee p si y solo si q, o también p equivale a q es verdadera cuando p y q tienen el mismo valor de verdad, es decir:

Para representar proposiciones emplearemos los símbolos p, q, r... o, lo que es lo mismo, emplearemos los símbolos p, q, r... como variables proposicionales.

FORMA DE UNA PROPOSICIÓN

Uno de los descubrimientos más sorprendentes con el que nos encontramos al estudiar lógica consiste en que la validez de una deducción depende exclusivamente de la forma que ésta tenga, y no del posible significado de las proposiciones que en ella intervienen.

Las proposiciones trabajo o no trabajo y estoy sentado o no estoy sentado tienen la misma forma  $p\lor \lnot p$: La tabla de verdad de esta forma proposicional $p\lor \lnot p$  es:

Es decir, cualquier proposición que tenga la forma $p\lor \lnot p$  será verdadera independientemente del valor de verdad que tenga p: La forma de las proposiciones va a estar determinada por la disposición de los conectivos $\left\{ \lnot ,\land ,\lor ,\Longrightarrow ,\Longleftrightarrow \right\} $; por lo que vamos a introducir la definición de forma proposicional para estudiar aquellas propiedades que únicamente dependen de la manera en la que están colocados dichos conectivos lógicos:

Definición: Llamaremos forma proposicional a cualquier expresión formada por:

a) variables proposicionales tales como p; q, r;…

 b) los conectivos lógicos  $\left\{ \lnot ,\land ,\lor ,\Longrightarrow ,\Longleftrightarrow \right\} $

 c) los paréntesis (,)

Y construida utilizando las siguientes reglas:

1. Cualquier variable proposicional es una forma proposicional

2. Si A y B son formas proposicionales, entonces también lo son

En la práctica se suelen suprimir los paréntesis en aquellos casos en los que al hacerlo no se produce ambigüedad. Señalar también que, como veremos luego, la regla 2 puede ser simplificada prescindiendo de algunos de los conectivos.

Ejemplo: La expresión

No es una forma proposicional (por ejemplo, porque comienza por un conectivo binario ) mientras que la expresión

Sí lo es porque sigue las reglas de su construcción.

Obsérvese que última forma proposicional puede ser representada sin ambigüedad suprimiendo paréntesis por

Cada forma proposicional tiene asociada una tabla de verdad, que recoge los distintos valores de verdad de la forma al asignar valores V y F a las distintas variables involucradas. La tabla de verdad asociada a una forma proposicional se puede construir sistemáticamente a partir del procedimiento empleado para construir dicha forma proposicional:

Ejemplo: Construcción de la tabla de verdad de la forma proposicional $\left( p\land \lnot q \right) \Longrightarrow r$ 

Lo primero es determinar los pasos seguidos en su construcción. Obsérvese que según las reglas de construcción de formas proposicionales siempre se tiene un último conectivo que va separando la parte de la derecha y la de la izquierda que son proposiciones más simples (con menos conectivos):

En segundo lugar, se construye la primera fila de la tabla teniendo en cuenta dichos pasos:

En tercer lugar, establecemos todas las posibles situaciones de verdad o falsedad de las primeras variables del enunciado que intervienen:

Finalmente se van rellenando el resto de las columnas teniendo en cuenta por una parte el significado de los conectivos lógicos $\lnot ,\land ,\lor ,\Longrightarrow ,\Longleftrightarrow $ y por otra, que cada vez que aparece una nueva variable proposicional es preciso comparar las situaciones de verdad o falsedad obtenidas con los dos posibles valores de verdad de la nueva variable proposicional:

EJERCICIOS

Construir las tablas de verdad de las siguientes formas proposicionales:

TAUTOLOGÍAS Y RAZONAMIENTOS VÁLIDOS

Definición. Una forma proposicional es una tautología si toma el valor V cualquiera que sea la forma en que asignemos los valores V ó F a las variables proposicionales que en ella intervienen. Una forma proposicional es una contradicción si toma el valor F cualquiera que sea la forma en que asignemos los valores V ó F a las variables proposicionales que en ella intervienen.

Ejemplo. $\left( p\Longrightarrow q \right) \Longleftrightarrow \left( \left( \lnot p \right) \lor q \right) $.   Es una tautología según se sigue de su tabla de verdad:

EJERCICIOS

Probar que las siguientes formas proposicionales son tautologías: