Teorema de Rouche-Frobenius
Resolver un sistema de ecuaciones es encontrar los valores de los xj para los que se cumplen todas las ecuaciones o concluir que el sistema no tiene solución. Un sistema de ecuaciones puede tener solución (compatible) o no tenerla (incompatible). Los sistemas compatibles pueden tener una solución (determinados) o infinitas soluciones (indeterminados). En resumen podemos clasificar los sistemas de ecuaciones lineales del siguiente modo:
Dado el sistema

Su matriz de coeficientes A y B su matriz ampliada

Teorema de Rouché-Frobenius
Permite conocer si un sistema de ecuaciones tiene solución a partir del estudio del rango de la matriz asociada al sistema (matriz de coeficientes A) y del rango de la matriz ampliada de éste (matriz B).
Ejemplos:
a) Un sistema de ecuaciones con tres incógnitas nos genera la siguiente matriz ampliada

Determinar:
a) Si el sistema es compatible o incompatible
b) Si es compatible determinar si es determinado o indeterminado.
Solución:
Vamos a obtener el rango de la matriz por el método de Gauss
Tomando la submatriz de sus incógnitas y calculando su rango:

Eliminando la fila 3 al restarla de la fila 2, tenemos que Rg(A)= 2
Ahora, vamos a determinar el rango de la matriz ampliada.

Nos ha quedado una fila llena de ceros. Por tanto, esta matriz tiene dos vectores linealmente independientes y como consecuencia, el otro vector es dependiente de los otros dos.
Los vectores V1 y V2 son independientes. Por tanto, calcular el número de vectores linealmente independientes y calcular el rango de la matriz es exactamente lo mismo. Así que, el rango de la matriz anterior es 2, ya que es el número de vectores linealmente independientes que tiene: Rg(B) = 2.
El número de incógnitas del sistema es tres y tanto el rango de A como el de B es 2, por lo tanto,

Por lo que se concluye que el sistema es compatible indeterminado y en consecuencia tiene múltiples soluciones.
b) Determinar si el siguiente sistema de ecuaciones lineales:

a. Es compatible o incompatible
b. Si es compatible determinar si es determinado o indeterminado.
Solución:
Expresión matricial:

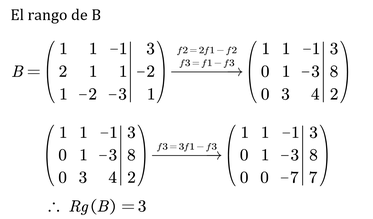
El número de incógnitas del sistema es tres y tanto el rango de A como el de B es 3, por lo tanto,

Por lo que se concluye que el sistema es compatible determinado y en consecuencia tiene una única solución.


