Mapas de Karnaugh
Introducción
La herramienta fundamental para la simplificación de funciones booleanas es y seguirá siendo el álgebra de Boole; sin embargo, como ya lo ha mostrado la experiencia, el álgebra de Boole tiene las siguientes desventajas:
- No es un método sistemático (no hay un algoritmo paso a paso a seguir).
- No es fácil saber cuándo la expresión ya está lo más reducida posible.
- Es fácil cometer errores y es difícil revisar el procedimiento.
Por ello, es importante contar con un método como el que se presentará aquí, el cual es un método sistemático y además gráfico, por lo cual es más sencillo y poderoso para la simplificación de funciones booleanas.
Sin embargo, previamente a la presentación del método se requieren algunas definiciones que se usarán de aquí en adelante.
Formas canónicas
Término Producto.- Se llama término producto una expresión booleana que solamente incluye operaciones AND entre sus variables (afirmadas o negadas)
Ejemplos de términos producto:
AB', ABC', BC, A'BCD', B, etc.
Forma SP.- Una función booleana se dice que está en la forma de suma de productos (SOP) si está formada exclusivamente por la suma (OR) de términos producto.
Ejemplos de funciones en forma SOP son:

Mintérmino- Es un término producto que contiene todas las variables de la función.
Ejemplos de minitérminos para una función de 4 variables A, B, C, D:
ABCD, AB’CD’, A ’BCD, etc.
Forma Canónica SOP.- Si los términos producto de una función booleana en la forma SOP son todos minitérminos, se dice que está en la forma canónica SOP.
Ejemplos de funciones en forma canónica SOP son:

Término Suma .- Se llama término suma a una expresión booleana que solamente incluye operaciones OR entre sus variables (afirmadas o negadas)
Ejemplos de términos suma:
A + B', A + B + C', B + C , A' + B + C + D'
Forma POS.- Una función booleana se dice que está en la forma de producto de sumas (POS) si está formada exclusivamente por el producto (AND) de términos suma.
Ejemplos de funciones en forma POS son:

Maxtérminos.- Son términos suma que contienen todas las variables de la función.
Ejemplos de maxtérminos para una función de 4 variables A, B, C, D son:
A + B + C + D , A + B + C' + D', A' + B + C + D
Forma Canónica POS.- Si los términos suma de una función booleana en la forma POS son todos maxtérminos, se dice que está en la forma canónica POS.
Ejemplos de funciones en forma canónica POS son:

Notación
Una manera de simplificar la escritura de las funciones en forma canónica consiste en representar sus términos por números binarios, en base a la siguiente convención


A la representación anterior se le llama notación en Lista de minitérminos.

A la representación anterior se le llama notación en Lista de maxtérminos.
Observación: El orden de las variables en la notación anterior debe coincidir con el orden en que están especificadas, es decir, f(A,B,C) ≠ f(B,C,A) ≠ f(A,C,B), etc.
Planteamiento de un circuito lógico
A partir de los conceptos y definiciones anteriores ya estamos en condiciones de plantear algunos diseños sencillos de circuitos lógicos. Podemos ordenar el procedimiento para esto de acuerdo a los siguientes pasos:
- Planteamiento de la función que debe hacer el circuito en una tabla de verdad.
- Obtención de la función en lista de minitérminos o de maxtérminos.
- Simplificación de la función lógica
- Implementación mediante compuertas lógicas de la función simplificada
Ejemplo:
Un jurado está formado por tres jueces A, B, C, cada juez emite su voto a favor oprimiendo un botón enfrente de él. Se desea construir un circuito que encienda una luz que indique si la mayor parte del jurado votó a favor y no la encienda en cualquier otro caso.

La función que realiza lo deseado es L(A,B,C) = ∑ m(3,5,6,7).
Usando álgebra booleana podemos simplificar la función como

Como habrá podido advertirse, en el procedimiento anterior, los únicos pasos que no han sido completamente sistematizados son el 1 y el 3 (la simplificación de la función).
A continuación se presenta un método sistemático para realizar este paso.
Minimización de funciones booleanas
Como ya se ha visto, la simplificación de funciones mediante el álgebra booleana puede ser una tarea difícil, ya que en el álgebra booleana no existe un procedimiento claro a seguir, uno debe buscar el camino para la simplificación en base a la intuición y la experiencia. Para realizar la simplificación de funciones eficientemente, presentaremos un método, llamado Mapas de Karnaugh, el cual es un método gráfico que proporciona una técnica estándar y sistemática en la reducción manual de funciones booleanas.
Mapas de Karnaugh
Los Mapas de Karnaugh (MK) no son más que una extensión de los conceptos de tablas de verdad, diagramas de Venn y minitérminos. A continuación se ilustrará la manera en que estos tres conceptos se entrelazan para obtener lo que llamaremos un Mapa de Karnaugh. Para ello, consideremos el Diagrama de Venn de dos conjuntos A y B y localicemos en el los subconjuntos o regiones correspondientes a los cuatro minitérminos A.B, AB, AB y AB, es decir, los minitérminos m0, m1, m2 y m3.
Como puede verse, Todo el diagrama de Venn se puede particionar en estas cuatro regiones independientes (no tienen puntos en común) y cada región está identificada por un minitérmino. Por otro lado, nada nos obliga a dibujar los conjuntos A y B redondos y el conjunto universo cuadrado.
Simplificación de circuitos lógicos :
El mapa es un diagrama hecho de cuadrados, en que cada cuadrado representa un minitérmino. Los cuadrados a los minitérmino que producen 1 para la función se marcan con un "1" y los restantes con "0" o se dejan vacíos. Para reconocer varios patrones y combinar cuadrados marcados por 1 en el mapa, es posible derivar las expresiones algebraicas alternas para la función, a partir de las cuales se puede seleccionar la más conveniente.
Los mapas para las funciones de dos, tres y cuatro variables se muestran en las siguientes figuras.


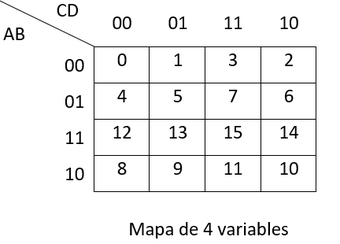
El número de cuadrados en un mapa de "n" variables es 2n minitérminos y son listados por un número decimal equivalente para fácil referencia. Los números de minitérminos son asignados en un arreglo ordenado de tal manera que los cuadrados adyacentes representen los minitérminos que difieren solamente en una variable. Los nombres de las variables son listados a través de ambos lados de la línea diagonal en la esquina del mapa. Los 1 y 0 marcados a lo largo de cada fila y de cada columna designan el valor de las variables. Cada variable debajo de los paréntesis contiene la mitad de los cuadrados en el mapa en donde aquella variable aparece sin comillas (no complementada). La variable aparece con una comilla (complementada) en la mitad de los cuadrados. Toda la información que aparece en los mapas de la figura, no siempre es necesaria, en esta oportunidad se muestra solamente a modo explicativo.
El minitérmino representado por un cuadrado es determinado de la asignación binaria de las variables a lo largo de los bordes izquierdo y superior del mapa. Note que el orden de las combinaciones no es binario natural, sino que es código Gray(00, 01, 11, 10), esto debido a que el funcionamiento del método se basa en combinaciones adyacentes.
A continuación se muestran algunos ejemplos de representación en mapa de Karnaugh de distintas funciones a partir de su tabla de verdad, este mapa representará los valores a minimizar cuando la función arroje un valor igual a 1.
a) Mapa de Karnaugh para representar dos variables

b) Mapa de Karnaugh para representar tres variables


c) Mapa de Karnaugh para representar cuatro variables


Metodología de reducción
Vamos a indicar cada uno de los pasos para obtener la expresión SOP (mínima suma de productos). Para ello vamos a ilustrarlo con el ejemplo:

Los pasos a seguir para conseguir reducir esta expresión son:
1. Convertir la expresión a una suma de productos si es necesario. Esto se puede realizar de varias maneras: Algebraicamente.
Construyendo una tabla de verdad, trasladando los valores al mapa de Karnaugh. Esta es la forma que vamos a utilizar.

2. Cubrir todos los unos del mapa mediante rectángulos de 2N elementos, donde N = 0 ... número de variables. Ninguno de esos rectángulos debe contener ningún cero (tal y como indicábamos en el apartado anterior).
Para minimizar el número de términos resultantes se hará el mínimo número posible de rectángulos que cubran todos los unos.
Para minimizar el número de variables se hará cada rectángulo tan grande como sea posible.

Véase que en este caso se han unido las celdas que contienen valor 1 para formar un único rectángulo, en cada caso, EL MÁS GRANDE POSIBLE.
3. Encontrar la MSP (suma de productos mínima). Atención porque podemos encontrarnos con que puede haber más de una MSP.
Cada rectángulo pertenece a un término producto.
Cada término se define encontrando las variables comunes en cada rectángulo rectángulo.

En nuestro ejemplo debemos buscar las variables comunes en cada rectángulo, por lo tanto tenemos: En el rectángulo azul el elemento común es Z’, y en el rectángulo rojo los elementos comunes son X’Y’, por lo tanto la función resultante es F(X, Y, Z) = X’Y’+Z’ .

Coloración y representación de cada celda en un mapa de karnaugh
Dos variables

Tres variables

Cuatro variables

Rectángulos y productos .
Cada rectángulo representa un término. El tamaño del rectángulo y el del término resultante son inversamente proporcionales, es decir que, cuanto más largo sea el rectángulo menor será el tamaño del término final.
En general, si tenemos una función con n variables :
Un rectángulo que ocupa una celda equivale a un término con n variables.
Un rectángulo que ocupa dos celdas equivale a un término con n-1 variables.
Un rectángulo que ocupa 2n celdas equivale al término de valor 1.
Por lo tanto, para encontrar el MSP se debe:
Minimizar el número de rectángulos que se hacen en el mapa de Karnaugh, para minimizar el número de términos resultantes.
Maximizar el tamaño de cada rectángulo, para minimizar el número de variables de cada término resultante.
Agrupación de rectángulos .
Cuando tenemos distintas posibilidades de agrupar rectángulos hay que seguir ciertos criterios:
Localiza todos los rectángulos más grandes posibles, agrupando todos los unos. Estos se llamarán implicantes primos.
Si alguno de los rectángulos anteriores contiene algún uno que no aparece en ningún otro rectángulo entonces es un implicante primo esencial. Éstos han de aparecer en el resultado final de manera obligatoria.
El resto de implicantes primos se podrán combinar para obtener distintas soluciones.

Véase este ejemplo que ilustra lo que les planteamos. Aquí los implicantes primos son cada uno de los diferentes rectángulos obtenidos. Los primos implicantes esenciales son el rectángulo azul y el verde, por contener unos que no son cubiertos por otros rectángulos. Así todas las posibles soluciones han de contener estos dos implicantes. Luego descartamos los rectángulos amarillo y morado para obtener como tercer componente de la solución el rectángulo rojo.
Solución: F( A, B, C, D ) = ABD+AB’C+A’C’
El procedimiento de diseño
Aunque en principio, al abordar el problema de diseño de un circuito podemos usar nuestra experiencia, intuición, inventiva y sentido común, todos estos elementos no nos garantizan una solución óptima. Sin pretender coartar la creatividad e imaginación del estudiante, se propone el siguiente Procedimiento de Diseño de Circuitos Lógicos :
Primer paso.- Identificar en el enunciado del problema las variables involucradas en el diseño, asignarles un símbolo y representarlas en un Diagrama de Bloques, el cual es un bloque desconocido interiormente aún, pero su exterior debe estar bien especificado, es decir, debe poseer un conjunto de entradas (variables independientes) y salidas (variables dependientes o funciones a diseñar).
Segundo paso.- Interpretar en el enunciado las relaciones de dependencia lógica entre entradas y salidas y representarlas en una Tabla de Verdad. Este paso debe realizarse cuidadosamente, dado la ambigüedad propia del lenguaje que puede llevar a relaciones lógicas equivocadas.
En este paso no debe olvidarse la relación directa de los conectivos gramaticales Y, O con las operaciones AND, OR respectivamente, así como la negación gramatical con el complemento lógico (NOT). Sin embargo, hay que ser cuidadoso de las interpretaciones gramaticales de O inclusivo (OR) y O exclusivo (EXOR). Esto ciertamente será más sencillo si el enunciado lo elaboramos nosotros mismos a partir de un problema real, pues nosotros sabremos exactamente lo que queremos decir, Sin embargo, en la mayoría de los casos abordados por un estudiante, los enunciados de los problemas los ha elaborado otra persona (el autor de un libro, o el profesor de la materia).
Tercer paso.- Obtener de la tabla de verdad los Mapas de Karnaugh, un mapa por cada variable de salida
Cuarto Paso.- Obtener las expresiones lógicas mínimas para cada variable de salida usando los mapas del paso anterior.
Quinto paso.- Dibujar la implementación con puertas lógicas procurando usar el mínimo de circuitos integrados.
En este paso hay que tener presente que una expresión lógica mínima NO garantiza una implementación mínima en términos de circuitos integrados. Para ello, se puede recurrir al uso de puertas lógicas de un sólo tipo , ya que esta estrategia permite aprovechar todas las puertas lógicas de cada circuito integrado utilizado. Las puertas que permiten ser utilizadas de esta manera son las puertas NAND o NOR. Las primeras son adecuadas para formas SP y las segundas para formas PS.
A continuación estos pasos se ilustrarán con un ejemplo.
Ejemplo
Diseñar un circuito para controlar el encendido y apagado de una lámpara, la cual deberá encender siempre que sea de noche, o la iluminación ambiental sea muy baja, a menos que se desee ahorrar energía.
El indicador de horario nocturno es una señal (N) controlada por un reloj (N = 1 indica que es de noche), El indicador de iluminación ambiental es una señal L controlada por una fotocelda (L=1 indica que aún hay luz ambiental) y la interfaz utiliza un par de conmutadores A, B para indicar si desea ahorrar energía, de manera que si ambos están desactivados (AB = 00) no se ahorrará energía, si sólo uno de los dos se activa bloqueará el encendido debido a L y, finalmente si ambos están activados la luz no se activará.
Solución.- Procedemos de acuerdo al procedimiento planteado, paso a paso:
Diagrama de bloques


Mapa de Karnaugh
F(A,B,N,L)= ∑m(0,2,3,6,7,10,11)


Función simplificada
De acuerdo con el M.K. anterior, obtenemos F= A’B’L’ + A’N + B’N

