Factorización de binomios

Factorización de la diferencia de dos cuadrados

Una diferencia de cuadrados corresponde al tercer producto notable, en consecuencia para factorizar una diferencia de cuadrados se obtiene el producto de dos binomios donde el primer término de cada binomio será la raíz cuadrada del primer término y el segundo término de cada binomio corresponde a la raíz cuadrada del segundo término de la diferencia. Uno de esos binomios sumará sus términos, mientras el otro los restará.

Ejemplo

Factorizar $9x^2-16y^2$

Se calcula la raíz cuadrada de cada uno de los términos, obteniendo:

$$\sqrt{9x^2}\ =3x\  \text{y}\ \sqrt{16y^2}\ =4y$$

Luego la factorización será: 

$$9x^2-16y^2=\left(3x+4y\right)\left(3x-4y\right)$$

Ejercicios

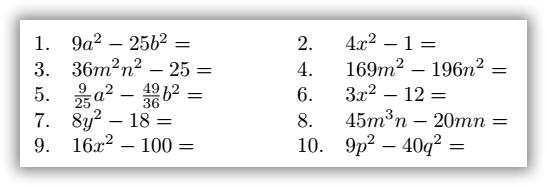
Diferencia de cubos

Cualquier diferencia de cubos puede factorizarse de la siguiente manera:

1. Se extrae la raíz cubica del primer término y también del segundo.

2. Luego se escriben dos paréntesis el primero con la resta de las raíces y el segundo de la forma siguiente, la primera raíz al cuadrado más el producto de las dos raíces más el cuadrado de la segunda raíz, como se indica a continuación:

$$a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)$$

Ejemplo

Factorizar $8-x^3=$

$$8-x^3=\left(2-x\right)\left(2^2+2x+x^2\right)=\left(4+2x+x^2\right)$$

Suma de cubos

Cualquier suma de cubos puede factorizarse de la siguiente manera:

1. Se extrae la raíz cubica del primer término y también del segundo.

2. Luego se escriben dos paréntesis el primero con la suma de las raíces y el segundo de la forma siguiente, la primera raíz al cuadrado menos el producto de las dos raíces más el cuadrado de la segunda raíz, como se indica a continuación:

$$a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)$$

Ejemplo:

Factorizar $27a^3+1=$

$$27a^3+1=\left(3a+1\right)\left(9a^2-3a+1\right)$$

Ejercicios