Desigualdades no lineales

Para resolver desigualdades con otras potencias mayores que 1 en la variables, utilizamos métodos de factorización y el siguiente principio.

Ejemplos: 

Resolver la desigualdad 

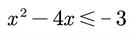
Seguimos el siguiente algoritmo:

1. Movemos a la izquierda todos los términos a la derecha del signo de desigualdad

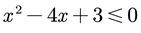
2. Factorizamos la expresión cuadrática

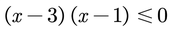
3. La expresión anterior nos dice que el producto de los binomios es cero o negativo. Para poder determinar el intervalo de solución debemos determinar el comportamiento de cada factor para los valores distintos a sus puntos críticos. Los puntos críticos son los valores donde cada factor se hace 0. 

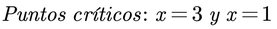
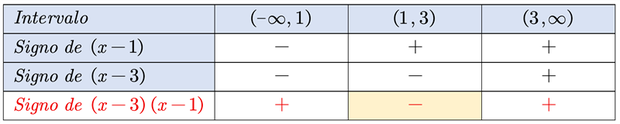
4. Construimos una tabla para determinar los signos de cada factor en cada intervalo. Al final determinamos el signo del producto o cociente de esos factores según la expresión original.

5. Solución.

La tabla nos indica que la inecuación es negativa o cero en el intervalo (1, 3), por lo tanto, la solución está dada por 

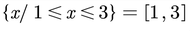
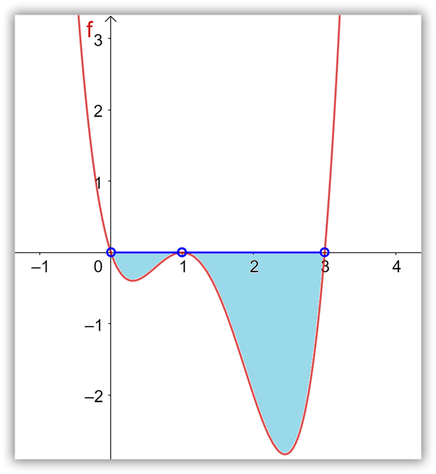
6. La solución gráfica se muestra a continuación

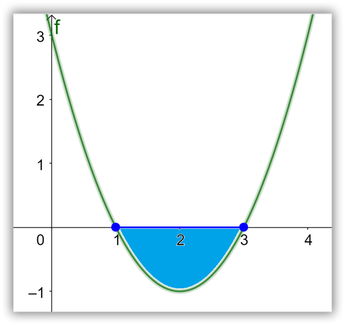
2. Resolver la inecuación

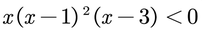
Solución:

Todos los términos distintos de cero se encuentran a la derecha del signo de desigualdad y la expresión ya se encuentra factorizada.

Procedemos entonces a determinar los puntos críticos y los intervalos de la inecuación. Considerando los tres factores, se tiene que estos se hacen cero cuando el valor de x es 0, 1 o 3. Por lo que esos tres números nos definen los intervalos en la recta de números reales X.

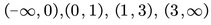
Generamos la tabla para determinar los signos

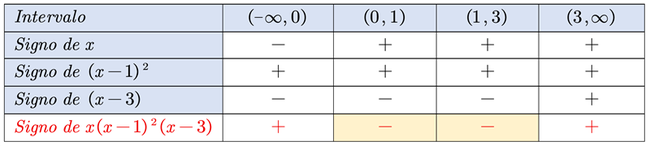
La inecuación es menor que cero en los intervalos (0,1) y (1,3). Por lo tanto la solución está dada por:

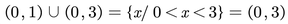
La solución gráfica se muestra a continuación

3. Resolver la inecuación

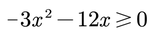
Seguimos el siguiente algoritmo:

1. Todos los términos distintos de cero se encuentran a la izquierda de desigualdad.

2. Factorizamos la expresión cuadrática.

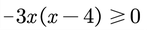
3. La expresión anterior nos dice que el producto de los binomios es cero o positivo. Para poder determinar el intervalo de solución debemos determinar el comportamiento de cada factor para los valores distintos a sus puntos críticos. Los puntos críticos son los valores donde cada factor se hace 0. 

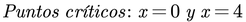
4. Construimos una tabla para determinar los signos de cada factor en cada intervalo. Al final determinamos el signo del producto o cociente de esos factores según la expresión original.

5. Solución. La tabla nos indica que la inecuación es positiva o cero en el intervalo (0, 4), por lo tanto, la solución está dada por

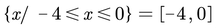
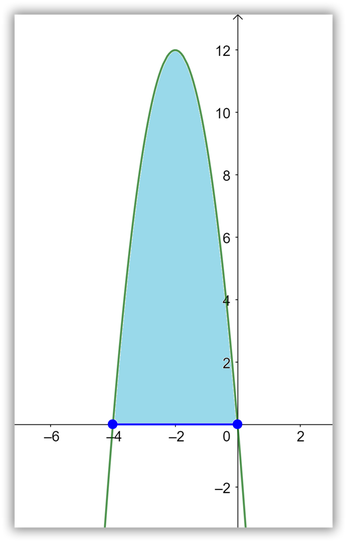
6. La solución gráfica se muestra a continuación