Entendemos como sistema de numeración al conjunto de símbolos y de reglas por medio de las cuales permitimos el conteo de elementos en un conjunto. Todo sistema numérico por tanto está conformado por un conjunto finito de símbolos, y un conjunto determinado y finito de reglas mediante las cuales combinarlos.

Los sistemas numéricos acompañan al hombre desde la antigüedad, y podemos asociar algunas civilizaciones con su propio sistema numérico. Entre ellos conocemos en la actualidad la existencia de sistemas numéricos propios de pueblos ancestrales como el egipcio, el mesopotámico y el maya entro otros más.

Los sistemas numéricos conocidos pueden clasificarse en tres tipos distintos: Sistemas no posicionales. Se caracterizan porque cada símbolo tiene asignado un valor fijo, sin importar la posición que ocupe dentro de la cifra. Ejemplos de ellos son por ejemplo el sistema egipcio y el sistema romano.

Sistemas posicionales. El valor de un símbolo está determinado tanto por el símbolo mismo y por la posición que ocupe dentro de la expresión numérica correspondiente, pudiendo valer más o menos o expresar distintos valores dependiendo de dónde se encuentre.

Otra manera de clasificar los sistemas de numeración muy difundida actualmente, está fundamentada en la base a la utilizada para sus cálculos. Así,  el sistema predominante en la actualidad es el sistema numérico decimal (cuya base es 10).

En el sistema numérico decimal, para representar los números se usan los 10 símbolos conocidos: 0, 1, 2, 3, 4, 5, 6, 7, 8 y 9. Al representar un número, la posición del símbolo es significativa; y su valor posicional se asigna desde la derecha y hacia la izquierda, el primer símbolo representa las unidades, el siguiente símbolo las decenas, el siguiente las centenas, y así sucesivamente.

Por ejemplo,

Teorema Fundamental de la Numeración. Considérese un sistema de numeración posicional de base x, x > ,1 entonces, cualquier otro numeral N se puede expresar, de la forma:

Siendo cada a_n un símbolo del sistema numérico.

Sistema numérico binario

El sistema binario, es un sistema de numeración en el que los números son representados utilizando únicamente dos símbolos: 0 (cero) y 1 (uno). Es uno de los sistemas utilizados en las computadoras electrónicas digitales de la actualidad.

En una computadora electrónica, los datos y las instrucciones se codifican como bits. El hardware de una computadora electrónica sustenta su estado en un circuito electrónico capaz de estar en uno y solo uno de dos estados: uno que representa a 1, y el otro a 0.

Conversión de números de un sistema numérico a otro

Para convertir un número de un sistema numérico a otro, por ejemplo, de sistema binario a sistema decimal o, al contrario, descomponemos en factores el número binario, de base 2, y así convertirlo en el equivalente del sistema decimal.

Si tenemos el número binario 1101101, representación que es factible expresar como:

Es factible generalizar la solución del ejemplo anterior para cualquier base arbitraria b, con el siguiente algoritmo.

Conversión de un entero base b en decimal

Este algoritmo nos mostrará el valor decimal del entero en base b

Entrada: c, n, b (donde c es el número de cifras, b es la base y n el número)

Salida: val_dec

Convertir_base10

{ int numero, base, numDigitos, aux, numB10

    numDigitos = 0, aux = 0, numB10 = 0

    escriba ("Digite un número entero y su base:")

    lea (numero,base)

    escriba("El número ", numero, " escrito en base ", base << " = ")

    mientras(numero > 0) {

        aux = numero / 10

        numero = numero - (aux * 10)

        numB10 = numB10 + numero * base^numDigitos

        numero = aux }

    Escriba(numB10," base 10")  

}

Código en C++

Sistema hexadecimal

El sistema hexadecimal (abreviado hex.) es el sistema de numeración posicional que tiene como base el 16. Así como el sistema decimal es parte integral en nuestra vida diaria, las tecnologías de la computación e informática y el procesamiento de datos se fundamentan en el sistema binario. Como ya lo hemos visto el sistema binario nos permite trabajar problemas complejos con dos estados: 0 y 1. Sin embargo, cuando se requieren números binarios grandes a menudo la codificación se vuelve incomprensible. En este caso, el sistema hexadecimal nos facilita la comprensión, puesto que la información que requiere 8 dígitos en el sistema binario se puede expresar con solo 2 números hexadecimales.

En principio, dado que el sistema usual de numeración es de base decimal y, por ello, solo se dispone de diez dígitos, se adoptó la convención de usar las seis primeras letras del alfabeto latino para suplir los dígitos que faltan. El conjunto de símbolos es el siguiente:

Nótese que las letras corresponden a los siguientes valores numéricos decimales:

A = 10, B = 11, C = 12, D = 13, E = 14 y F = 15

En algunos casos se usan indistintamente letras minúsculas en lugar de mayúsculas. Como en cualquier sistema de numeración posicional, el valor numérico de cada dígito depende de su posición en la cadena de dígitos, quedando multiplicado por una cierta potencia de la base del sistema, que en este caso es 16.

Ejemplo: 

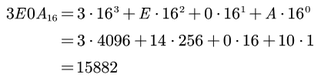
Si deseamos extender el código en C++ del programa anterior para obtener en base 10 un número digitado en base 16, es necesario modificar el programa.

En primer lugar, es condición necesaria invertir la cadena leída, ya que está será introducida como una cadena.

Luego se hará la conversión carácter a carácter para obtener el número en base 10, para ello utilizaremos el siguiente fragmento de código.

Finalmente uniendo con el programa principal obtendremos

Algoritmo para el cambio de base decimal a cualquier otra base

Un algoritmo para obtener el correspondiente número a otro en base decimal es el de la aproximación por potencias de la base. 

Así por ejemplo si deseamos expresar números como 15 o 32 o 111 en su equivalente binario entonces:

Así por ejemplo si vamos a determinar el equivalente en base 2 de un número decimal, buscamos la potencia 2ⁿ , que cuando supere el número natural dado, tomemos el exponente menos uno y determinemos el resto.

El exponente encontrado nos muestra la cota superior de la serie hasta el número de potencias de 2 que irán adicionándose hasta que el exponente sea 0.

Cada una de estas potencias es factor de los correspondientes coeficientes del conjunto B= {0,1}, cuya suma corresponde al número decimal dado.

 Para cualquier p ∈ N el número que deseamos transformar a una base k, donde kⁿ<= p < kⁿ⁺¹,  los exponentes de p serán entonces E={0,1,...,n} .

Donde   s = Σ c_i·k^e , con e=0,1,2,…n, y donde cada c_i ∈ {0,1,…k-1}.

El algoritmo para obtener el correspondiente número en base k, está dado por:

// convertir Decimal a Base N

Int iteraciones(int nBase, int nNum) {

    int cont = 0

    mientras (nBase^cont < nNum){

        cont++   

    }

    return cont - 1

}

void conversionBasal(int nBase, int nNum, int it) {

    int cociente = 0, resto = 0, limite = it

    int potencia = 0, aux = nNum

    char auxCoc = 'Z', auxRes = 'Z'

    mientras(limite > 0) {

        potencia = (int)(pow(nBase, limite))

        cociente = aux / potencia

        resto = aux % potencia

        aux = resto

        limite--

    }

inicio

{  int numDecimal = 0, base = 0;

    escriba("Digite el número decimal y la base a convertir ")

    leer  numDecimal, base

    escriba("El número decimal ", numDecimal, " en base ", base,  " = "

    int cont = iteraciones(base, numDecimal)

    conversionBasal(base, numDecimal, cont)

}