Relaciones y dígrafos
RELACIONES
Una relación R de A en B es cualquier subconjunto de A x B. Si , entonces se dice que “x está relacionado con y” y se escribe x R y o R(x, y).
La notación infija x R y es muy común en matemática, por ejemplo, para decir que 3 y 5 están vinculados por la relación “menor que” se escribe 3 < 5. La notación prefija R(x, y ) a veces se usa sin paréntesis, como R xy .
Si A = B entonces en lugar de “relación de A en A” simplemente se dice “relación en A”.
El conjunto de todas las relaciones de A en B es el conjunto P(A x B ).
Ejemplo 1. Sea F = {Ana, Berta, Carlos, Diana, Ernesto} una familia en la cual Ana es la madre de Berta, Berta es la madre de Carlos y Diana, y Diana es la madre de Ernesto.
Entonces M = {(Ana, Berta), (Berta, Carlos), (Berta, Diana), (Diana, Ernesto)} es una relación de F en F que corresponde al concepto intuitivo de la relación “es madre de”.
Ejemplo 2. Sean A y B conjuntos de números reales. Se define la siguiente relación R (de igualdad) de A a B:
a R b si y solo sí a = b
Ejemplo 3. Sea A = {1, 2, 3, 4, 5}
Defina la siguiente relación R (menor que) en A:

Ejemplo 4. $Sea\,\,A=\mathbb{Z}^+$ el conjunto de todos los enteros positivos. Muestre un ejemplo y un contraejemplo de la siguiente relación R en A:

Ejemplo 5. Una línea aérea da servicio a cinco ciudades c1, c2, c 3, c4 y c5. La tabla muestra el costo en dólares del viaje de ci a cj. En consecuencia, el viaje de c1 a c3 es de $100, mientras que el costo del viaje de c4 a c2 es de $200.

Defina la siguiente relación entre el conjunto de ciudades A: ci R cj si y sólo sí el costo de ir de ci a cj es menor o igual a $180. Determine R.
R = {(c1,c2),(c1 ,c3),(c1,c4),(c2,c4),(c3,c1),(c3 ,c2),(c4 ,c3),(c4 ,c5),(c5,c2),(c5,c4)}
CONJUNTOS QUE SURGEN DE LAS RELACIONES
Sea $R\subset AxB$ , una relación de A a B. Se va a definir ahora varios conjuntos importantes y útiles relacionados con R.
El dominio de R, denotado Dom(R), es el conjunto de todos los elementos de A que están relacionados con algún elemento de B. En otras palabras, Dom(R), un subconjunto de A, es el conjunto de todos los primeros elementos de los pares que forman R. De modo similar, se define el rango de R, designado por Ran(R), como el conjunto de todos los elementos de B que están relacionados con algún elemento de A.
Los elementos de A que no están en Dom(R) no están involucrados en la relación R de manera alguna. Esto es cierto también para los elementos de B que no están en el rango de R.
Ejemplo 6. Si R es la relación definida en A = {1, 2, 3} y B = {r, s} t.q. su relación es
R = {(1,r),(2,s),(3,r)}
Entonces el Dom(R) = A y Ran(R) = B.
Ejemplo 7. Sea A = {1, 2, 3, 4, 5} Definida por la siguiente relación R (menor que) en A:

Entonces el Dom(R) = {1, 2, 3, 4} y Ran(R) {2, 3, 4, 5}
Teorema 1. Sea R la relación de A a B, y sean A1 y A2 subconjuntos de A. Entonces:

Teorema 2. Sean R y S relaciones de A a B. Si R(a) = S(a) para todas las a de A, entonces R = S.
LA MATRIZ DE UNA RELACIÓN
Es posible representar una relación entre dos conjuntos finitos como una matriz de la siguiente manera. Si A = {a 1, a 2, … , a m } y B = {b1, b 2, … , b n} son conjuntos finitos que contienen m y n elementos respectivamente, y R es una relación de A a B, se representa R por la matriz m x n MR [m ij ], la cual se define por

La matriz MR se llama matriz de R. A menudo MR proporciona una manera fácil de verificar si R tiene una propiedad dada.
Ejemplo 8. Sea R la relación definida en A = {1, 2, 3} y B = {r, s} t.q. su relación es
R = {(1,r),(2,s),(3,r)}
Entonces la matriz de R es:

A la inversa, dados los conjuntos A y B con |A|=m y |B|=n, una matriz m x n cuyas entradas son ceros y unos, determina una relación.
Ejemplo 9. Considere la matriz

DÍGRAFOS
Si A es un conjunto finito y R es una aplicación sobre A, también se puede representar R gráficamente como sigue. Se traza un círculo para cada elemento de A y se marca el círculo con el elemento correspondiente de A. A estos círculos se los llama vértices. Se traza a continuación una flecha, a la flecha se le llama lado o arco, del vértice ai al vértice aj si y solamente sí ai R aj. La representación gráfica resultante de R se llama gráfica dirigida o dígrafo de R.
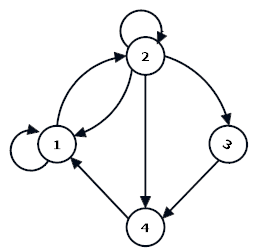
Ejemplo 10. Sean
A = {1, 2, 3, 4}
B = {(1,1), (1,2), (2,1), (2,2),(2,3),(2,4),(3,4),(4,1)}
Entonces el dígrafo de R es el siguiente:
Ejemplo 11. Encuentre la relación determinada por el siguiente dígrafo.

Un concepto importante para las relaciones es el que inspira la forma visual de los dígrafos. Si R es una relación sobre un conjunto A y $a\in A$, entonces el grado interno de a (relativo a R) es el número $b\in A\,\,t.q. \left( b,a \right) \in R$. El grado externo de a es el número $b\in A\,\,t.q. \left( a,b \right) \in R$.
Esto significa en términos del dígrafo de R, que el grado interno de un vértice es el número de arcos que terminan en el vértice y el grado externo de un vértice es el número de arcos que salen del vértice.
Ejemplo 12. Considere el dígrafo del ejemplo 9. Determinar los grados internos y externos de cada vértice.

Ejemplo 13. Sea A = {a, b, c, d} y sea R la relación sobre A que tiene la matriz

Construya el dígrafo de R, y haga una tabla de los grados internos y grados externos de todos los vértices.


Ejemplo 14. Sea A = {1, 4, 5}, y sea R la relación que da el dígrafo siguiente.
Encuentre MR y R.


TRAYECTORIAS EN RELACIONES Y DÍGRAFOS
Supóngase que R es una relación sobre un conjunto A. Una trayectoria de longitud n en R de a a b es una secuencia finita , que comienza con a y termina con b, tal que:

Debe observarse que una trayectoria de longitud n involucra n+1 elementos de A, aunque no necesariamente distintos.

Ejemplo. Considere el dígrafo de la siguiente figura.
Entonces:
π1: 1, 2, 5, 4, 3 es una trayectoria de longitud 4 del vértice 1 al vértice 3.
π2: 1, 2,5,1 es una trayectoria de longitud 3 del vértice 1 al vértice 1.
π3: 2, 2 es una trayectoria de longitud 1 del vértice 2 al vértice 2.
Una trayectoria que inicia y termina en el mismo vértice se llama ciclo. En el ejemplo anterior, π2 y π3 son ciclos de longitud 3 y 1 respectivamente. Es claro que una trayectoria de longitud 1 se identifica como un par ordenado (x, y) que pertenece a R.
Se define una relación Rn sobre A como sigue: $xR^ny$ significa que hay una trayectoria de longitud n de x a y en R. También puede definirse una relación $R^{\infty}$ sobre A , suponiendo que $xR^{\infty}y$ signifique que hay una trayectoria en R de x a y. La longitud de esa trayectoria dependerá, en general, de x y y . A la relación $R^{\infty}$ se le llama relación de conectividad de R.
Ejemplo: Sea A = {1, 2, 3, 4, 5, 6}. Sea R la relación cuyo dígrafo aparece a continuación.



Ejemplo: Sean A = {a, b, c, d, e} y R = {(a, a), (a, b), (b, c), (c, e), (c, d), (d, e)}


Luego:
(a) a R2 a a puesto que a R a y a R a
a R2 b puesto que a R a y a R b
a R2 c puesto que a R b y b R c
b R2 e puesto que b R c y c R e
b R2 d puesto que b R c y c R d
c R2 e puesto que c R d y d R e
(b) Para calcular $R^{\infty}$, se necesitan todos los pares ordenados de vértices para los cuales haya una trayectoria de cualquier longitud del primer vértice al segundo.

