Redes de Petri
Las Redes de Petri son una teoría matemática postulada por el alemán Carl Adam Petri que proporciona una herramienta gráfica y matemática de modelado para la descripción formal de sistemas cuya dinámica se caracteriza por la concurrencia, sincronización, exclusión mutua y conflictos, las cuales son características típicas de sistemas distribuidos. Al disminuir el precio del hardware de computadora, y de los procesadores en particular, existe un creciente interés en el procesamiento concurrente, para lograr mayor velocidad y eficiencia.
Las redes de Petri como herramienta para especificar sistemas de tiempo real, reconocen un antecedente en las máquinas de estado, una de las primeras técnicas para modelar arquitecturas de sistemas de cómputo, basada en la descripción de un sistema mediante los conceptos de estado y transición.
Esta técnica de especificación se basa en establecer una completa relación entre el comportamiento de entrada/salida de una máquina y la variación de sus estados internos, dando una idea de la ocurrencia de las transiciones en respuesta a cada una de las posibles entradas.
Estos estados son representados mediante círculos. Un arco desde el estado s al estado s etiquetado a/b significa que en el estado s con una entrada a la máquina cambiará al estado s obteniendo b como salida. Un alfabeto de entrada define las entradas desde el mundo externo, mientras un alfabeto de salida define las salidas de la máquina al mundo externo.
La salida de esta máquina depende tanto de la entrada actual como del estado actual. Un caso especial de la especificación de la salida es que ésta puede depender sólo del estado actual. De esta manera, el estado está asociado con un símbolo de salida particular, aunque varios estados podrían mapearse sobre la misma salida.
Los sistemas de computadora son con frecuencia muy complejos, largos, y con varias componentes que interactúan. A pesar de la diversidad de sistemas que queremos modelar se pueden señalar varios puntos en común. Una idea fundamental es que los sistemas están compuestos de módulos o componentes separadas, e interactuantes. Cada componente puede ser en sí misma un sistema, pero su comportamiento puede ser descripto en forma independiente de los otros módulos del sistema, excepto por interacciones bien definidas con las otras componentes. Cada componente tiene su propio estado. El estado es una abstracción de la información relevante necesaria para describir sus (futuras) acciones.
Por otra parte, los sistemas a menudo exhiben situaciones de concurrencia o paralelismo. Las actividades de una componente de un sistema pueden ocurrir simultáneamente con las de otros módulos. Dado que las componentes de los sistemas interactúan, es necesario que haya sincronización. Esto puede resultar en que una componente esté esperando a otra. El temporizado de acciones de distintos módulos puede ser muy complejo y las interacciones resultantes entre las componentes pueden ser difíciles de describir.
La gran limitación de las máquinas de estado se presenta cuando se intentan modelar sistemas con acciones simultáneas. Si bien podrían representarse cada una de estas acciones simultáneas como máquinas de esta- do y luego intentar unirlas, esta unión no es simple. Se genera un aumento importante en el número de estados lo que dificulta el manejo y la claridad del diagrama de estados resultante.
La representación de la concurrencia y la sincronización presentes en un sistema es más natural utilizando Redes de Petri en lugar de una máquina de estado, debido a que las mismas poseen un paralelismo inherente.
Características de una Red de Petri
La teoría de Redes de Petri puede ser aplicada a diversas áreas, y sus fundamentos se están convirtiendo en un tema casi "obligatorio" para los científicos en computación, analistas de sistemas e ingenieros.
Los conceptos básicos de la teoría de Redes de Petri pueden ser entendidos con una mínima base de conocimientos. Sin embargo, las Redes de Petri abarcan muchos aspectos de la ciencia de computación y las matemáticas. Una apreciación y entendimiento completo de la teoría de Redes de Petri requiere una buena base en el estudio de lenguajes formales y autómatas, sistemas operativos, arquitectura de computadoras y álgebra lineal.
Las Redes de Petri son una herramienta útil para el estudio de sistemas. La teoría permite que un sistema sea modelado por una Red de Petri, una representación matemática del sistema. El análisis de la Red puede revelar importante información acerca de la estructura y el comportamiento dinámico del sistema modela- do, la que puede ser usada para evaluarlo y sugerir mejoras o cambios.
Definición. Una red de Petri es una gráfica dirigida que está formada por lugares y transiciones, unidos alter- nativamente por arcos dirigidos. Un lugar puede o no contener marcas. El conjunto de marcas asociadas a cada uno de los lugares en un momento dado, constituye un marcado de la red. Para la descripción funcional de sistemas concurrentes los marcados representan estados y las transiciones sucesos, que dependen del cumplimiento de determinadas condiciones.
Definiciones
Estructura de una Red de Petri
Una Red de Petri consta de cuatro partes: un conjunto de lugares P, un conjunto de transiciones T, una función de entrada I, y una función de salida O. Las funciones de entrada y de salida relacionan transiciones y lugares. La función de entrada I es un mapeado desde una transición t a una colección de lugares I(t ), conocida como los sitios de entrada de la transición. La función de salida O mapea una transición t en una colección de sitios O(t ), conocida como los sitios de salida de la transición.
DEFINICIÓN: Una estructura de Red de Petri, C, es una 4-upla, C = (P,T,I,O) tal que:
P = {p , p ,...., p } es un conjunto finito de lugares o plazas no vacío.
T = {t , t , ...., t } es un conjunto finito de transiciones no vacío.

Una red de Petri es ordinaria si sus funciones de incidencia sólo pueden tomar valores 0 y 1, es decir (todos sus arcos son de peso unitario).
Una red de Petri es generalizada si sus funciones de incidencia pueden tomar cualquier valor entero mayor o igual que cero.
Una red de Petri es pura o no reflexiva si ninguna plaza es a la vez entrada y salida de una misma transición.
Representación. Toda herramienta de modelado tiene una o más formas de ser representada. En el caso de las redes de Petri, podemos encontrar una representación gráfica y otra matricial.

Representación gráfica
Una red de Petri puede asociarse con un grafo dirigido con dos clases disjuntas de nodos, los lugares y las transiciones.
Un círculo representa un lugar, una barra representa una transición y un arco dirigido conecta lugares y transiciones.
Algunos arcos van desde un lugar a una transición y otros desde una transición a un lugar. Un arco dirigido desde un lugar p a una transición t define p como un lugar de entrada para t. Un lugar de salida se indica con un arco desde la transición al lugar.
Los arcos se etiquetan con sus pesos (enteros positivos). Si una de esas etiquetas se omite, significa que el arco tiene peso uno.
Las marcas se representan como puntos negros en los lugares. Los lugares que contienen marcas se consideran lugares activos.
A las transiciones se les asocia eventos (funciones lógicas de las variables de entrada). Una transición se dice que está sensibilizada cuando todos sus lugares origen están marcados.
Cuando ocurre un evento asociado a una transición, se dice que la transición está validada.
Una Red de Petri es un multígrafo, dado que permite arcos múltiples desde un nodo del grafo a otro. Además, dado que los arcos son dirigidos, es un multígrafo dirigido. Dado que los nodos del grafo pueden ser particionados en dos conjuntos (sitios y transiciones), tal que cada arco está dirigido de un elemento de un conjunto a un elemento del otro conjunto, es un multígrafo dirigido bipartito.
El hecho de que las dos representaciones sean equivalentes significa que dada cualquiera de ellas, es posible encontrar la otra y además es única.
Marcas de las Redes de Petri: Una marca µ es una asignación de tokens (puntos negros) a los sitios de una Red de Petri. El número y posición de los tokens puede cambiar durante la ejecución de una Red de Petri.
DEFINICIÓN: Una marca µ de una Red de Petri C = (P,T,I,O) es una función que va desde el conjunto de sitios P a los enteros no negativos N.
La marca µ también puede definirse como un n-vector, μ = (μ1,μ2, ....,μn),donde n = |P| y cada µi ∊ N, i = 1,...,n. El vector µ da para cada sitio pi en una Red de Petri el número de tokens en ese sitio. El número de tokens en el sitio pi es µi , i = 1,...,n. Las definiciones de marca como función y como vector están relacionadas por µ(pi) = µi.
Una Red de Petri marcada M = (C,µ) es una estructura de Red de Petri C = (P,T,I,O) y una marca µ.
En un grafo de Red de Petri, los tokens se representan por puntos dentro de los círculos que representan los sitios. En la figura puede verse una Red de Petri marcada.

Dado que el número de tokens o marcas que puede ser asignado a un sitio de una Red de Petri es ilimitado, hay una infinidad de marcas para una Red de Petri. El conjunto de todas las marcas para una Red de Petri con n sitios es el conjunto de los n-vectores, Nn . Este conjunto, aunque infinito, es numerable. El estado de una red de Petri marcada se define por el número mi de marcas contenidas en cada plaza pi y se representa por su marcado.
Ejecución
Una red de Petri se ejecuta de acuerdo con las siguientes reglas.
1) Una transición t se dice que está habilitada en una red de Petri con un marcado M si todas sus plazas de entrada contienen al menos tantas marcas como arcos haya desde cada plaza a la transición, esto es, si M(p)≥I(p,t) para toda plaza de entrada de la transición t.
Una transición sin plazas de entrada, lo que se denomina transición fuente, está siempre habilitada puesto que no tiene restricciones de entrada.
2) Una transición habilitada puede dispararse retirando de cada plaza de entrada tantas marcas como arcos haya desde la plaza hacia la transición (I(p,t)) y depositando tantas marcas en cada plaza de salida como arcos haya desde la transición a la plaza (O(t,p)). La selección de cuál entre todas las transiciones habilitadas es la próxima en dispararse es arbitraria y se supone que se decide en un nivel de abstracción inferior.
3) El disparo de una transición modifica la distribución de marcas en las plazas. Si, desde un marcado Mi, se produce el disparo de una transición t, el nuevo marcado que se obtiene, Mj, se calcula mediante la expresión:
Las marcas se utilizan para definir la ejecución de la red de Petri. Una transición sin lugares de salida, lo que se denomina transición sumidero, elimina marcas de la red de Petri.
Marcado
Las marcas son indivisibles; esto es, una marca puede quitarse de una plaza por sólo una transición. Esto hace que el disparo de una transición pueda deshabilitar otras transiciones retirando las marcas de las plazas de entrada compartidas. Exceptuando esta restricción, el disparo de las transiciones se desarrolla de una manera asíncrona.
Un marcado Mj se dice que es inmediatamente alcanzable desde un marcado Mi si Mj puede obtenerse disparando una transición habilitada por Mi.
Un marcado Mk se dice que es alcanzable desde un marcado Mi si existe una secuencia de disparo de transiciones que transforma Mi en Mk.
El conjunto de alcanzabilidad, R(M), de una red de Petri marcada es el conjunto de todos los marcados alcanzables desde M.
Ejemplo: Evolución del marcado en una Red de Petri

Árbol de alcanzabilidad
El árbol de alcanzabilidad de un RdP representa el conjunto de todas las marcas alcanzables desde el marcado inicial M0.
Consiste en un grafo en forma de árbol en el que cada nodo es una marca alcanzable de la red y los nodos se conectan mediante arcos etiquetados con la transición que se dispara para pasar de un marcado a otro.
Partiendo del estado inicial M0, se generan todos los estados alcanzables desde éste mediante el disparo de una transición. A partir de cada estado, se vuelve a repetir el proceso, apareciendo, en consecuencia, un grafo en forma de árbol con una estructura infinita.
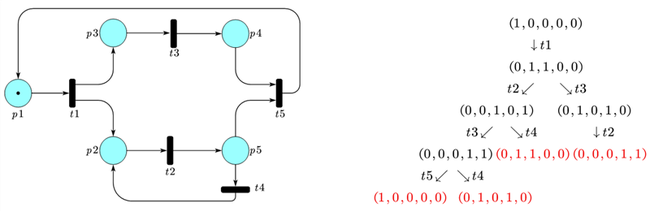
Recuérdese que el disparo de las transiciones es arbitrario, por lo que lo mostrado en rojo depende del orden en que se ejecutaron los disparos de las distintas transiciones.
Para representar esta estructura infinita con un árbol finito, se deja de expandir el árbol cuando se alcanza una marca frontera (hojas del árbol). Éste es el que verifica alguna de las siguientes condiciones:
a) Es un marcado muerto, esto es, un marcado en el que no hay ninguna transición habilitada.
b) Es un marcado que ya ha aparecido en el árbol de alcanzabilidad, lo que se denomina nodo duplicado.
c) Es un marcado que sólo se diferencia de otro presente en el árbol por tener un número distinto de marcas en algún lugar y que habilita el mismo conjunto de transiciones que el primero.
Estos marcados se representan con una w en la posición correspondiente a la plaza con distinto número de marcas. Así, el árbol de alcanzabilidad de cualquier RdP es finito.
Representación matricial
Una transición tiene un determinado número de lugares de entrada (o precondiciones) y de lugares de salida (o postcondiciones). Cada uno de estos se puede representar por una matriz binaria de dos dimensiones, donde las columnas representan los lugares o plazas, las filas las transiciones y las celdas la conexión entre ambas. Las matrices reciben los nombres de “Matriz de incidencia previa” y “Matriz de incidencia posterior” respectivamente.
Entre las técnicas de análisis más usadas se encuentran las ecuaciones matriciales, donde se definen dos matrices C y C para representar las funciones de entrada y salida. Cada matriz tiene m filas (una por cada transición) y n columnas (una por cada lugar).
Se definen:
C-[j,i] = I(pi, tj) (Matriz de incidencia previa)
C+[j,i] = O(pi, tj) (Matriz de incidencia posterior)
La forma matricial de definición de una Red de Petri (P, T, C- , C+ ) es equivalente a la forma estándar pero permite que las definiciones sean reexpresadas en términos de vectores y matrices.
Matriz de incidencia de N: C = C+ − C- .
Si consideramos que C- corresponde a la función IN (Entrada), y C+ a la función OUT (salida).
El grafo G=(P,T, I, O, V) asociado a la RdP=(P, T, IN, OUT), está definido de la siguiente forma:

Se denomina a:
I(t): conjunto de lugares de entrada a la transición t.
O(t): conjunto de lugares de salida a la transición t.
I’(p): conjunto de transiciones de entrada al lugar p.
O’(p): conjunto de transiciones de salida al lugar p.
V(p, t): valor del arco que va de p a t.
V(t, p): valor del arco que va de t a p.
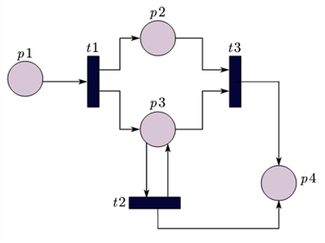
En el ejemplo anterior representado con el siguiente grafo, tenemos:
M0 definida como el vector columna (1,0,0,0,0)
|
I(t1)={p1} |
O(t1)={p2,p3} |
I’(p1)={t5} |
O’(p1)={t1} |
|
I(t2)={p2} |
O(t2)={p5} |
I’(p2)={t1,t4} |
O’(p2)={t2} |
|
I(t3)={p3} |
O(t3)={p4} |
I’(p3)={t1} |
O’(p3)={t3} |
|
I(t4)={p5} |
O(t4)={p2} |
I’(p4)={t3} |
O’(p4)={t5} |
|
I(t5)={p4,p5} |
O(t5)={p1} |
I’(p5)={t2} |
O’(p5)={t4,t5}
|
Por regla general en los arcos de valoración 1 se omite su escritura y tienen valoración cero los arcos ausentes en la red. Por lo tanto en la RdP anterior todos los arcos tienen valoración 1. Además el vector M0 nos indica que el lugar 1 posee marca.
Por lo tanto las matrices de incidencia son las siguientes:

Ejemplo:
Dada la Red Petri R1 = (P, T, I, O, M0), donde:
P = {p1, p2, p3, p4}, T = {t1, t2, t3 }, Mo=(5, 0, 0, 0)
Ejemplo:
Dada la Red Petri R2 = (P, T, I, O, M0), donde:
P = {p1, p2}, T = {t1, t2, t3 }, Mo=(5,1). El grafo correspondiente es el siguiente

Al modelar una situación, los lugares representan condiciones, las transiciones representan eventos, y la presencia de al menos un elemento en un lugar (condición) indica que tal condición se cumple.
Una transición t ∈ T está sensibilizada (habilitada) para un marcado M dado,
Si y solo si ∀p ∈ •t se verifica M(p) ≥ Pre(p, t).
El grado de habilitación de una transición indica el máximo número que la transición puede ser disparada concurrentemente.
Regla de evolución del marcado: Si t está habilitada para un marcado M entonces t puede dispararse. En la operación se alcanza un nuevo marcado M0, y se denota por M[t] > M0, el cual resulta de quitar Pre(p, t) marcas de cada lugar p ∈ •t y añadir Post(t, p) marcas a cada lugar p ∈ t •.
El cambio en el marcado está dado por la ecuación:
M0(p) = M(p) − Pre(p, t) + Post(t, p), ∀p ∈ P
Cada disparo de una transición modifica la distribución de las marcas, y por ello produce un nuevo marcado en la red.
Siguiendo con el ejemplo 1, al disparar la transición t1, obtenemos:

Estructuras básicas
Selección: Selecciona el proceso a ejecutar
Atribución: Ejecución independiente de un proceso por dos procesos distintos
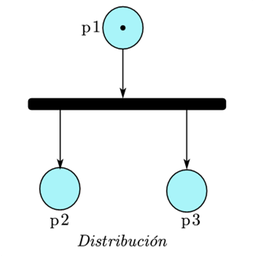
Distribución: Ejecución de procesos paralelos o concurrentes
Conjunción: Sincronización de procesos en paralelo

Ejecución Secuencial: La transición t2 puede ser disparada solamente si antes es disparado t1

Sincronización: La transición t1 estará habilitada para ser disparada si todos los nodos de entrada de la transición t1 poseen al menos una marca en cada uno de ellos

Concurrencia: Las transiciones t2 y t3 son concurrentes. Con esta propiedad, la RdP es capaz de modelar sistemas de control distribuido con múltiples procesos ejecutándose concurrentemente.
Conflictos: Tanto la transición t1 como t2 están listas para ser disparadas, pero el disparo de alguna de ellas produce que la otra transición quede inhabilitada para ser disparada.
Definición: En una red de Petri, si una arista va del lugar p a la transición t, decimos que p es un lugar de entrada para la transición t. Un lugar de salida se define de manera análoga. Si cada lugar de entrada de una transición t tiene al menos un elemento, decimos que t está activada. La descarga de una transición elimina un elemento de cada lugar de entrada y agrega un elemento a cada lugar de salida.
Definición: Si una serie de descargas, transforma un marcado M en un marcado M’, decimos que M’ es alcanzable desde M.
Entre las propiedades más importantes estudiadas en la teoría de redes de Petri están la supervivencia y la seguridad. La supervivencia se refiere a la ausencia de estancamientos y la seguridad se relaciona con la capacidad limitada de la memoria.
Definición: Un marcado M de una red de Petri está vivo si, partiendo de M, si importar la serie de descargas realizadas, es posible descargar cualquier transición dada mediante alguna secuencia de descargas adiciona- les. Si un marcado está vivo, sin importar la serie de descarga de transiciones, P nunca se estancará.
Definición: Un marcado M para una red de Petri está acotado si existe algún entero positivo n con la propiedad de que, en cualquier secuencia de descarga, ningún lugar recibe más de n elementos. Si un marcado M está acotado y en cualquier secuencia de descarga ningún lugar recibe más de un elemento, decimos que M es un marcado seguro.
Si cada lugar representa un registro capaz de guardar una palabra de computadora y si un marcado inicial es seguro, tenemos garantizado que no se excederá la capacidad de memoria de los registros.
Propiedades
En las RdP podemos encontrar propiedades estructurales, que dependen de la estructura topológica de las RdP, independientes del marcado inicial y, las propiedades de comportamiento que sí dependen del marcado inicial.
Propiedades estructurales
Rdp pura
Una RdP N es una red pura si no existe ninguna transición que tenga un lugar que sea al mismo tiempo de entrada y salida de la transición:
Red de Petri acotada estructuralmente
Una red de Petri está acotada estructuralmente si está acotada para cualquier marcado inicial finito.
Un lugar p en una red de Petri se dice no acotado estructuralmente si existe un marcado M y una secuencia de disparo σ desde M tal que p no esté acotado.
Red de Petri estructuralmente viva
Una red de Petri está estructuralmente viva si existe algún marcado inicial para el que está viva.
Red de Petri completamente controlable
Una red de Petri se dice completamente controlable si cualquier marcado es alcanzable desde cualquier otro marcado.
Red de Petri estructuralmente conservativa
Una red de Petri es estructuralmente conservativa si, para cualquier marcado inicial M0 y un marcado
Propiedades de comportamiento
Vivacidad
Una transición t está viva para un marcado inicial dado M0, sii existe una secuencia de disparos a partir de un marcado M sucesor de M0 que comprenda a t :

Una RdP marcada está viva para M0 sii todas sus transiciones son vivas para M0.
Se puede decir que la propiedad de vivacidad significa la ausencia en el conjunto de alcanzabilidad de un marcado en el que la red se bloquee totalmente (deadlock), ya que, para que esté viva, todas sus transiciones deben ser disparables desde cualquier marcado alcanzable.
Se dice que una RdP marcada está parcialmente viva para M0 si, tomando como punto de partida cualquier marcado alcanzable a partir de M0, existe al menos una transición disparable y otra transición no viva. Toda RdP marcada parcialmente viva tiene la posibilidad de evolución global, independientemente de que existan transiciones que no puedan ser disparadas.
Ejemplo: una red de Petri no viva.
Para la secuencia de disparos t1, t2, t1 , t2 , no hay bloqueo. Si ahora se disparan las transiciones t1 , t3 , t4 , ya no se puede disparar ninguna transición más, la red queda “bloqueada”.
Ciclicidad
Se dice que una RdP posee un comportamiento globalmente cíclico para M0 si existe una secuencia de disparos que permite alcanzar el marcado inicial M0 a partir de cualquier marcado M alcanzable a partir de M0: ∀M ∈ M(R, M0), ∃σ tal que M σ→M0.
La ciclicidad o reversibilidad de una RdP marcada garantiza que no existen subconjuntos finales de estados (marcados). Un subconjunto final de estados (marcados) contiene estados (marcados) mutuamente alcanzables entre sí y tales que el estado inicial (marcado inicial) no es alcanzable a partir de ninguno de ellos.
Ejemplo de una red no reversible
Esta RdP es pseudoviva, además no tiene la propiedad de reversibilidad ya que el marcado inicial no se puede obtener jamás.


Acotamiento
El significado de esta propiedad es el de asegurar que el sistema que una red representa posee un número finito de estados (si suponemos que cada lugar de la red representa a una variable de estado del sistema y su marcado el valor de dicha variable). Luego la propiedad de acotamiento determina la finitud del número de estados del sistema representado por una RdP.
Un lugar p es k-acotado para M0 sii existe un número entero k tal que M(p) ≤ k para cualquier marcado M ∈ M(R, M0). Se denomina cota del lugar p al menor entero k que verifica la desigualdad anterior.
Una RdP marcada es k-acotada para M0 sii todos sus lugares son k- acotados para M0:
∀p ∈ P y ∀M ∈ M(R, M0), M (p) ≤ k.
Merece una consideración especial la 1-acotación. Si una RdP es 1- acotada para M0 , su marcado es binario (un lugar está o no está marcado) y se dirá que la RdP es binaria para M0. Una red segura, es una RdP 1- acotada. Una RdP es estructuralmente acotada si es acotada para cualquier marcado inicial y finito.
Se dice que la red está k-acotada si para todo marcado alcanzable tenemos que ningún lugar tiene un número de marcas mayor que k. Las redes 1-acotadas son conocidas como binarias.
Si la red diseñada generar más marcas que las que su acotación permite el modelado será erróneo.

Alcanzabilidad
La alcanzabilidad es una base fundamental para estudiar las propiedades dinámicas de cualquier sistema. Al dispararse una transición habilitada, esta cambiará la distribución de las señales (marcado). De esta forma, de una secuencia de disparos resultará una secuencia de marcados, luego un marcado Mn es alcanzable a partir de M0, si existe una secuencia de disparos que a partir de M0 nos lleve a Mn. Una secuencia de disparos la denotaremos por σ = t1, t2,....., tn . en este caso Mn es alcanzable desde M0, sii ∃ σ t.q. M0 [ σi Mn.

La exclusión mutua
Cuando varios procesos comparten algún recurso del sistema tal que cuando uno de ellos lo está usando los demás no pueden hacerlo, debe implementarse un mecanismo de espera cuando el recurso compartido está siendo usado. La manera de hacerlo es utilizar un sitio para representar la condición "el recurso compartido está libre". En la figura se muestra la solución:
Este sitio actúa como un "semáforo", sincronizando el acceso de los procesos al recurso compartido. El esquema es válido cualquiera sea el número de procesos que compartan el recurso. El primero que lo tome, quita la marca del lugar representativo del recurso disponible y entonces cualquiera que lo requiera deberá esperar. En este esquema no hay prioridades asignadas a los procesos que compiten simultáneamente por el uso del recurso.

El problema del productor y el consumidor
Aquí también existe un recurso compartido pero no para ser usado por los procesos sino como mecanismo de comunicación entre ellos. Entre un proceso que produce y otro que consume lo producido se puede instalar un depósito intermedio (buffer) con el fin de "amortiguar" las diferencias ocasionales de velocidad. Disponiendo un sitio para indicar la condición "depósito con producto", el proceso productor depositará un token cada vez que tenga un nuevo producto y el proceso consumidor comenzará su tarea cada vez que estando listo para ello, haya por lo menos un token en el depósito (figura de la derecha).
La limitación de este esquema es que no es capaz de representar un buffer de capacidad finita, pudiendo crecer el número de productos en el depósito sin límite en el caso de detención del proceso consumidor. En la figura siguiente se muestra la solución cuando se quiere acotar la cantidad de productos intermedios. Se muestra también un sistema compuesto por un productor y un consumidor operando en forma asincrónica, comunicándose mediante un buffer con capacidad para tres productos. El sitio "buffers llenos" representa la existencia de productos disponibles y el sitio "buffers vacíos" la cantidad de lugares disponibles en el depósito. Siempre se da que la suma de las marcas de ambos sitios, dan la capacidad total del depósito.
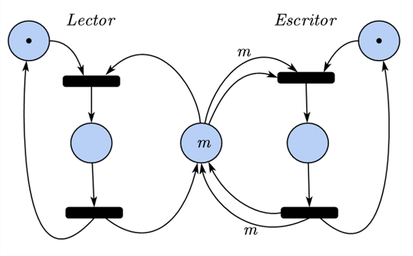
El problema de la lectura y la escritura
Esta situación se presenta en sistemas en el que un cierto número de tareas pueden realizar lecturas y/o escrituras sobre un área de memoria compartida en forma simultánea. A fin de asegurar la consistencia de la información, la ejecución de una escritura es excluyente, en tanto que se admitirá la ejecución concurrente de dos o más lecturas. En la figura se muestra una solución cuando el número de lectores es conocido e igual a "n" (observar la utilización de un semáforo con marca "m" y dos arcos también con capacidad igual a "m")
Ambientes para la especificación y verificación con redes de Petri
Como ya hemos señalado, además de contar con técnicas que permitan especificar sistemas es importante que luego de realizar la especificación se realice una validación o una verificación del modelo desarrollado.
Con un modelo de Redes de Petri podemos realizar una verificación del sistema propuesto, ya que mediante la ejecución de la red es posible obtener una simulación del comportamiento del sistema.
Es conveniente notar que generalmente logramos una verificación de la arquitectura propuesta, ya que una validación implica la utilización de un lenguaje más formal (aunque utilizando técnicas de análisis y la visión matemática de Redes de Petri podemos tener una "prueba" más cercana a una validación).
En este punto, es importante destacar la necesidad de desarrollar ambientes para especificar y verificar sistemas usando Redes de Petri, dado que cuando el modelo crece se torna inadecuado realizar manual- mente la ejecución de la Red. Por esto, el objetivo es obtener herramientas de software que permitan la ejecución automática de una especificación.
En el caso de las Redes de Petri, estas herramientas pueden orientarse hacia una definición gráfica, una definición estructural, o una combinación de ambas.
Los ambientes gráficos poseen la ventaja de permitir una rápida visión global del sistema que se especifica, aunque con frecuencia el hecho de tener que realizar una definición interactiva se torna un tanto tedioso. Además, si la red especificada es de un tamaño considerable el gráfico puede no ser todo lo claro que uno desea.
Cuando se opta por una definición orientada a la estructura podemos obtener un intérprete. En este caso, aunque se pierden las bondades de la especificación gráfica, el hecho de definir la red a modo de "seudocódigo" nos acerca a la derivación del código del sistema en lenguajes como ADA o Modula.
De todas maneras, cualquiera sea la opción elegida, el ambiente que se desarrolle debe proveer facilidades para especificar, ejecutar automáticamente, y verificar los sistemas.
Ejemplo:
Modelar el programa de computadora dado
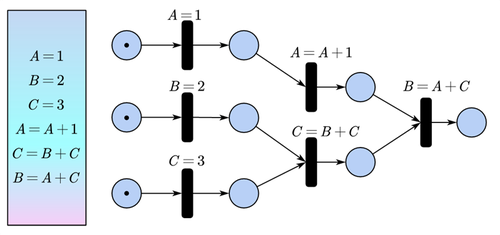
Ejercicios
1. Construya una red de Petri para especificar el funcionamiento de una máquina expendedora de bebidas. La misma tiene un depósito de bebidas con una cierta carga inicial, y un depósito de monedas el cual inicialmente se encuentra vacío. Cuando se le ingresa una moneda y hay bebidas, la máquina entrega una bebida y almacena la moneda en el depósito correspondiente. ¿Cómo modelaría la situación de que cuando no hay más bebidas la máquina retorne la moneda?
2. Existen pequeñas diferencias entre los sistemas de luces de tránsito en diferentes países. Por ejemplo, el sistema de luces alemán tiene una fase extra en su ciclo. Las luces no cambian repentinamente de rojo a verde sino que antes de pasar al verde enciende la luz verde junto con la luz amarilla. Construya una red de Petri que se comporte como el sistema de luces de tránsito alemán. Asegúrese que la red no permita transiciones que no son posibles.
3. Representar mediante el simulador HPetriSim (http://www.winpesim.de/) el sistema de atención de clientes en un restaurante. El cliente realiza un pedido a un mozo. Para que el pedido sea atendido, el mozo debe estar libre. Una vez realizado el pedido, el cliente debe esperar hasta que el plato solicitado sea preparado. Considerar que para que el plato esté listo, debe ingresar en la cocina, habrá un tiempo de preparación y recién entonces estará listo. Una vez que el plato está listo y el mozo libre, será servido al cliente que recién entonces podrá comenzar a comer. Indicar sitios, transiciones y una marcación posible.
4. Realizar, utilizando el simulador HPetriSim, la representación del control de llenado de un tanque mediante una Red de Petri. El tanque posee un sensor de baja (Sb) que se activa cuando el nivel de agua es menor al mínimo admisible y un sensor de alta (Sa) que se activa si el nivel de agua alcanza el máximo permitido. La descarga de agua se realiza a través de la apertura de una válvula (V) y el llenado del tanque proviene de una cisterna a través de una bomba hidráulica (B). Es condición necesaria que la cisterna esté llena de agua para que la bomba pueda encenderse (B on). De lo contrario la bomba se mantendrá apagada (B off).
5. Para las redes de Petri especificadas en la Figuras (a) y (b), se pide:
a) Obtener su árbol de alcanzabilidad.
b) Obtener sus matrices de incidencia previa C–, incidencia posterior C+, y de incidencia C.
c) A partir de su representación matricial, obtener los marcados que se obtienen para la red de Petri de la figura 1 (b) con las secuencias de disparo t1-t2-t3-t4-t1-t2-t3 y t1-t2-t3-t4-t2-t3-t4.












