Ecuaciones diofánticas
Se llama ecuación diofántica a cualquier ecuación algebraica con coeficientes enteros, de la que nos interesa exclusivamente las soluciones que tenga dentro del conjunto de los números enteros.
El origen del término diofántico hay que buscarlo en el matemático Diofanto de Alejandría, que vivió en el siglo III, y que se ocupó de este tipo de ecuaciones.
Como base previa al tema es importante recordar algunos conceptos de teoría de números, iniciaremos con el tema del Máximo Común Divisor.
Todos conocemos el método que se nos enseña en el colegio para ello: Descomponemos en factores primos los dos números y tomamos los factores comunes a ambos con el menor exponente con el que aparezcan.
Aunque es un método bastante útil y sencillo para conseguirlo que queremos tiene un evidente problema: si los números son muy grandes, o si sus factores primos lo son, la situación se puede complicar ya que el cálculo de la descomposición se torna bastante tedioso.
Por ello es interesante tener a mano otro método para casos en los que el procedimiento inicial se complique. Para ello utilizaremos el algoritmo de Euclides.
Algoritmo de Euclides
Para calcular el máximo común divisor de dos números enteros positivos a y b, dividimos el mayor, que puede ser a, entre el menor, supongamos b. Esta división nos proporcionará un cociente y un resto. Si aplicamos repetidamente el algoritmo del cociente, se obtiene:
Entonces, el máximo común divisor entre a y b es el último resto distinto de cero que obtengamos en el procedimiento anterior.
Ejemplo:
Determinar el mcd(721, 448)
Aplicando el algoritmo de Euclides, tenemos:

Ejemplo:
Determinar el mcd(12378, 3054)

Identidad de Bézout
La identidad de Bézout, es un teorema elemental de Teoría de números, siendo a y b dos enteros distintos de cero, y siendo d su máximo común denominador, existen dos enteros x, y tales que:

Simbólicamente tenemos que:

Propiedades
- Si a, b son enteros, no nulos, tal que mcd(a, b) = d, y sea c un entero cualquiera, entonces:

- Si d = mcd(a, b) entonces d es el menor entero de la forma ax + by con x, y enteros.
- Si d = mcd(a, b) entonces mcd(ma, mb) = md para todo m > 0
- Si d = mcd(a, b) entonces mcd(a/d, b/d) = 1
- Si mcd(a, b) = 1 y a|c y b|c entonces ab|c
- Si mcd(a, b) = 1 y a|bc entonces a|c
- Dos enteros a y b son primos entre sí (coprimos) sí y sólo sí

Ejemplo:
1. Dados (150, 39). Hallar x, y.
Aplicando el algoritmo de Euclides

Luego aplicamos el Lema de Bézout

Ecuaciones diofánticas lineales
El problema anterior, se escribe algebraicamente de la siguiente manera:
En la película La Jungla de Cristal 3, para desactivar una bomba, se propone el siguiente problema que consiste en colocar sobre una báscula controlada por computadora exactamente 4 galones de agua disponiendo únicamente de una garrafa de 5 galones y otra de 3 galones. ¿Cómo lo pueden conseguir?
Este problema lo que plantea es cuántas veces se debe llenar o vaciar la garrafa de 5 galones y/o llenar o vaciar la garrafa de 3 galones, para poder tener exactamente 4 galones.
Este problema nos genera lo que llamamos una ecuación diofántica
Son ecuaciones de la forma ax + by = c con coeficientes enteros, y de las que solamente nos interesan sus soluciones enteras.
El problema anterior, se escribe algebraicamente de la siguiente manera:

Una ecuación diofántica lineal es una ecuación de la forma:

Teorema:
Una ecuación lineal diofántica de la forma ax +by = n tiene solución entera x0, y0 si y solo si el máximo común divisor de a y b es divisor de n.
Además si llamamos d al mcd(a, b) se tiene que una solución particular de dicha ecuación puede obtenerse de la siguiente forma:
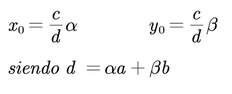
Los valores obtenidos en el teorema anterior son una solución particular de la ecuación.
Para obtener la solución general de una ecuación diofántica lineal enunciamos el siguiente teorema.
Teorema:
Si x0, y0 son números enteros y constituyen una solución particular de la ecuación

Entonces todas la soluciones enteras xy de la misma, son de la forma:

La solución de una ecuación diofántica es una consecuencia del algoritmo de Euclides y de la identidad de Bézout.
Ejemplo:
Encontrar la solución de la siguiente ecuación diofántica:

Algoritmo de Euclides

Aplicando la identidad de Bézout

Las soluciones particulares son

Si la ecuación tiene solución, entonces tiene infinitas soluciones y son de la forma:

Ejemplo:
Encontrar la solución de la siguiente ecuación diofántica:

Algoritmo de Euclides

Aplicando la identidad de Bézout

Las soluciones particulares son

La solución general está dada por:


Ejemplo:
La patrulla de la policía municipal de una ciudad ha impuesto sanciones de tráfico por valor de 3.700 U.M. (Unidades Monetarias). Si la sanción por exceso de velocidad es de 600 U.M. y la sanción por aparcamiento indebido es de 250 U.M, ¿cuántas sanciones ha impuesto de cada uno de los dos tipos?
Solución:

Solución Particular

Solución General

Para valores mayores que 0
Verificamos para x

Luego tenemos que para k=30 los valores obtenidos en la solución general son: x = 2 y=10. Por lo tanto se sancionaron 2 excesos de velocidad y 10 faltas de aparcamiento.


