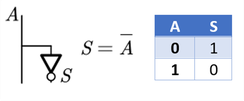Algebra Booleana
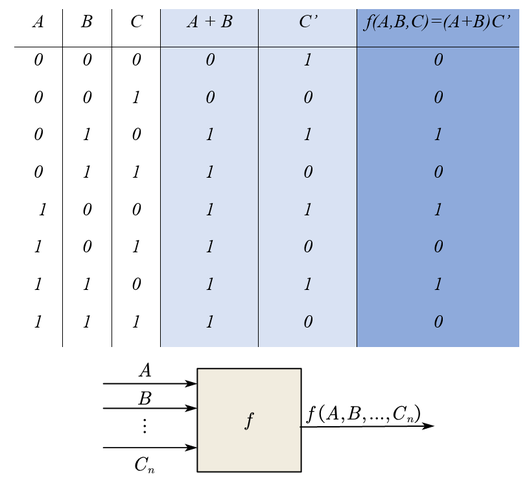
Las tablas que enumeran los valores de una función f para todos los elementos de Bn, como la que se muestra en la figura (a), con frecuencia son llamadas tablas de verdad para f. Esto se debe a que son similares a las tablas empleadas en lógica. Suponga que los xk representan proposiciones, y f(x1, x2,..., xn) representa un enunciado compuesto construido a partir de los xk. Si piensa que el valor 0 para un enunciado significa que el enunciado es falso, y que 1 significa que el enunciado es verdadero, entonces las tablas, como la de la figura (a), muestran la forma en que la verdad o falsedad de f(x1, x2,..., xn) depende de la verdad o falsedad de los enunciados xk que lo componen. Así, tales tablas son llamadas, con frecuencia, tablas de verdad, incluso cuando surgen en áreas distintas de la lógica, como en las álgebras booleanas.
La razón de la importancia de tales funciones es que, como se muestra de manera esquemática en la figura (b), pueden ser utilizadas para representar los requisitos de salida de un circuito para los posibles valores de entrada. Así, cada x, representa un circuito de entrada capaz de transportar dos voltajes indicadores (un voltaje para 0 y un voltaje distinto para 1). La función f representa la respuesta de salida deseada en todos los casos. Tales requisitos ocurren en la etapa de diseño de los circuitos computacionales combinatorios y secuenciales.
Observe con cuidado que la especificación de una función sólo enumera los requisitos del circuito. No indica cómo cumplir estos requisitos. Una forma importante de producir funciones de Bn a B es mediante el uso de polinomios booleanos, los cuales son considerados a continuación.
Polinomios booleanos
Sea x1 , x2,... ,xn un conjunto de n símbolos o variables. Un polinomio booleano p(x1 , x2,... ,xn) en las variables xk se define de manera recursiva como sigue:
x1 ,x2,... ,xn son todos polinomios booleanos.
Los símbolos 0 y 1 son polinomios booleanos.
Si p(x1 , x2, …, xn) y q(x1, x2, …, xn) son dos polinomios booleanos, entonces también lo son
No existen polinomios booleanos en las variables xk distintos de los que pueden ser obtenidos aplicando las reglas 1, 2, 3 y 4.
Los polinomios booleanos también reciben el nombre de expresiones booleanas.
Compuertas Lógicas. Las compuertas lógicas son dispositivos que operan con aquellos estados lógicos mencionados anteriormente y funcionan del siguiente modo, se ingresan los datos a un dispositivo y este “responde ” mediante una operación ( o serie de operaciones) con un resultado.
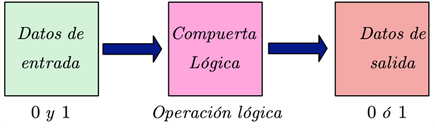
Cada una de las compuertas lógicas se las representa mediante un Símbolo, y la operación que realiza (Operación lógica) se corresponde con una operación lógica y una tabla, llamada Tabla de Verdad.
Compuerta not
Invierte el dato de entrada, por ejemplo; si la entrada es 1 (nivel alto) se obtiene en la salida un 0 (o nivel bajo), y viceversa.
Esta compuerta dispone de una sola entrada. Su operación lógica es S igual a A invertida.
El símbolo genérico para obtener una entrada o salida invertida o negada, es agregarle un círculo vacío al cable de salida o entrada.
Compuerta and
Una compuerta AND tiene dos datos de entrada como mínimo y su operación lógica es un producto entre ambas, no es un producto aritmético, aunque en este caso coincidan. La salida (resultado) es siempre una (es decir un único valor 0 ó 1).
Si la compuerta AND tuviera n datos de entrada, para obtener un 1 como resultado todos los datos de entrada debieran ser igual a 1
Compuerta or
Al igual que la anterior posee dos entradas como mínimo y la operación lógica, es la suma entre ambas. Aquí es bueno detenerse porque al lector cuando vea la tabla de verdad podrá observar que 1 + 1= 1. El tema es que se trata de una compuerta O Inclusiva. Es decir, basta que uno de los datos de entrada sea 1 para que su salida sea también 1*
Vemos la siguiente tabla de verdad.
Si la compuerta OR tuviera n datos de entrada, para obtener un 1 como resultado alguna de las de entrada debe ser igual a 1. Esto es:
En algunos textos o compendios de Álgebra Booleana, se presentan otros conectores o compuertas lógicas, las que se omiten ya que se pueden construir a partir de las tres anteriores.
Ejemplo
Ejemplo
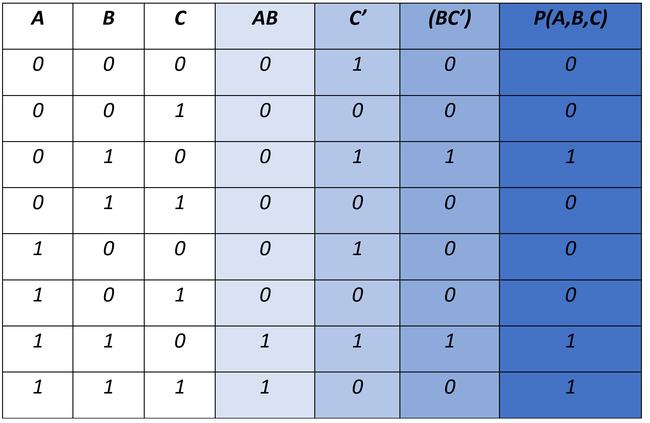
Dado el siguiente circuito, obtener la función de salida.
Solución: