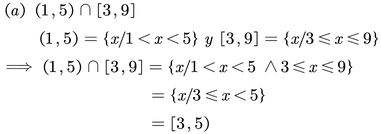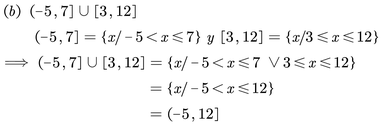Conjuntos e intervalos
Un conjunto es una colección de elementos con características similares considerada en sí misma como un objeto. Los elementos de un conjunto, pueden ser personas, objetos, colores, meses, días y cualquier otro grupo de elementos.
Se dice que un elemento pertenece al conjunto si está definido como incluido de algún modo dentro de él. Si P es un conjunto, la notación significa que a es un elemento de P, así mismo si escribimos quiere decir que x no es elemento de P.
Ejemplo: el conjunto de los números enteros es:

Por lo tanto, podemos escribir que:

Así, por ejemplo, si queremos escribir el conjunto de números enteros positivos menores que 7 por extensión, entonces lo expresamos de la siguiente forma:

Los conjuntos se pueden denotar de dos formas, éstas se denominan ‘Por extensión’ y ‘Por comprensión’. Si por el contrario lo queremos escribir por comprensión, entonces debemos escribirlo de la siguiente forma enunciando la única característica válida para ese y solo ese conjunto.

La notación anterior se lee: A es el conjunto de todas las x tales que x es un número entero mayor que cero y menor que 7.
Si M y N son dos conjuntos cualesquiera, la unión de los conjuntos M y N se expresa simbólicamente así:

que es el conjunto que está formado por todos los elementos que están en M o N o en ambos.
La intersección de dos conjuntos P y Q, se denota
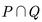
que es el conjunto de todos los elementos que están en P y Q, de otra forma es el conjunto formado por los elementos que tienen en común P y Q.
Ejemplo:

Intervalos en el conjunto de los números reales
Algunos subconjuntos en el conjunto de los números reales, se denominan intervalos y generalmente son representados geométricamente en segmentos de recta.
Todo intervalo tiene dos Extremos que pueden ser, por ejemplo: a y b, el intervalo está constituido por todos los puntos x tal que x está entre a y b, pudiendo ser a o b.
Los extremos pueden estar contenidos o no en el intervalo, así entonces según la pertenencia de los extremos los intervalos pueden clasificarse como: abiertos, cerrados y semiabiertos.
Por su longitud los intervalos pueden ser Finitos o Infinitos.
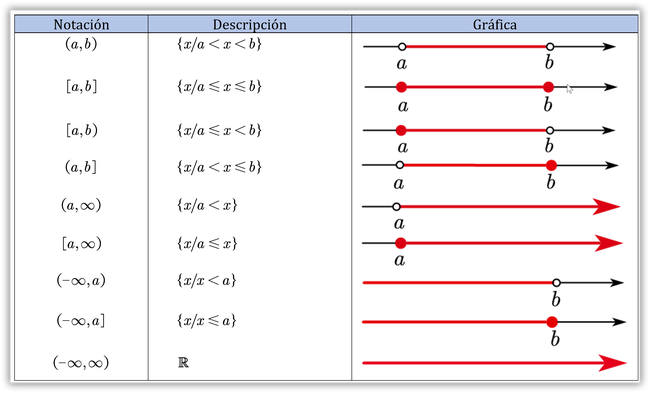
Notación
Para los intervalos cerrados se usa []
Para los intervalos abiertos (), < >,] [
Semiabiertos combinando los dos casos anteriores

Nótese que los paréntesis redondos indican que los extremos NO están incluidos en el intervalo, mientras que los corchetes indican que los extremos están incluidos en el mismo.
La siguiente es una lista de posibles tipos de intervalos.
Ejemplos:
Exprese cada intervalo como una desigualdad y grafique el mismo

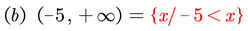
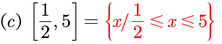
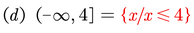




Uniones e intersecciones de intervalos
Graficar cada una de las siguientes expresiones