Inecuaciones de primer grado

Desigualdad: se llama desigualdad a toda relación entre expresiones numéricas o algebraicas unidas por uno de los cuatro signos de desigualdad <, >,$\ \le,\ \geq$ .

Las inecuaciones de primer grado con una incógnita son las que responden a las siguientes formas básicas:

Resolver una inecuación consiste en encontrar el valor o valores que la verifican, al contrario de las ecuaciones de primer grado, las inecuaciones tienen infinitas soluciones agrupadas en un conjunto.

Así por ejemplo, Las siguientes son desigualdades que involucran a la variable x.

Así por ejemplo la siguiente expresión es una desigualdad:

En la tabla adjunta verificamos algunos valores que satisfacen la inecuación y algunos que no la satisfacen.

Resolver una desigualdad que contenga una variable es encontrar todos los valores de la variable que satisfagan como verdadera la desigualdad. Con relación a una ecuación la diferencia es que la desigualdad por  lo general tiene infinito número de soluciones, por lo que se suele representar gráficamente.

Para resolver desigualdades usamos las siguientes reglas. Nótese que si tenemos que el coeficiente de la variable es negativo entonces multiplicamos los dos miembros de la inecuación por un número negativo (-1), lo que cambia el sentido de la relación en la inecuación.

Solución de una desigualdad

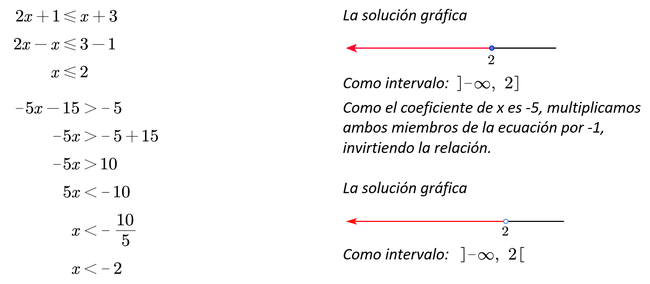
Resolveremos y graficaremos la solución de la siguiente desigualdad

Ejemplos

Resolver las siguientes inecuaciones

Ejercicios

En cada caso encuentre el conjunto solución como intervalo y la solución gráfica de cada inecuación.

Inecuaciones de primer grado con dos variables

Son aquellas en las que las variables que intervienen están elevadas a un exponente igual a la unidad.

Expresión general: son de la forma ax + by < c y todas sus equivalentes en la relación de orden, a saber:

Representan zonas del plano cartesiano. O bien dividen al plano en zonas.

Método de resolución: Se trata en el fondo de ecuaciones de rectas que debemos resolver y luego analizar las zonas del plano en que se cumple la desigualdad inicial.

Para las inecuaciones de la forma ax+by < c, determinamos la ecuación lineal a partir de la cual se genera la inecuación y la zona del plano que limita: y = mx + b, despejando de modo adecuado.

Ésta no es más que la ecuación de una recta en el plano, la cual divide al mismo en dos semiplanos. Uno de esos semiplanos contiene los puntos tales que y > mx+b y el otro los puntos tales que y < mx + b. Se trata pues de determinar qué puntos son los que cumplen la desigualdad o inecuación previa.

Para ello:

Dibujamos la recta, una vez dibujada tomamos un punto x del eje de abscisas cualquiera y trazamos la perpendicular por el mismo.

El punto en que ésta corta a la recta es tal que y = mx+b, prolongando la perpendicular encontraremos los puntos tales que y > mx+b, y por debajo estarán los que cumplen la condición y < mx+b.

Ejemplo

Sea la inecuación 2x + y > 4 

Al no satisfacer la relación, la solución se encuentra en el otro semiplano.

Ejemplo

Graficar la solución de 2x – y ≤ 2

En este caso procedemos a expresar la ecuación de la recta que limitará la región en dos semiplanos, dado que la variable y está precedida del signo de resta en la inecuación, multiplicamos por (-1) ambos términos de la misma e invertimos la relación así tenemos:

En este caso se satisface la relación, por lo que el punto (0,0) está contenido en el semiplano de la solución. Nótese que para hacer esta verificación es indistinto si tomamos la inecuación original o la inecuación multiplicada por -1.

Ejercicios

Resolver las siguientes inecuaciones con dos incógnitas