Operaciones con conjuntos
UNIÓN DE CONJUNTOS
Se llama UNIÓN de dos conjuntos A y B al conjunto formado por los elementos de A o de B, es decir:

Ejemplo:
Sean A = {a, b, c, d, e, f} y B={b, d, r, s}
Entonces $A\cup B$ está formado por todos los elementos que pertenecen a A o a B.
Luego,

INTERSECCIÓN DE CONJUNTOS
Se llama INTERSECCIÓN de dos conjuntos A y B al conjunto formado por objetos que son elementos de A y de B, es decir:
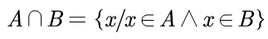
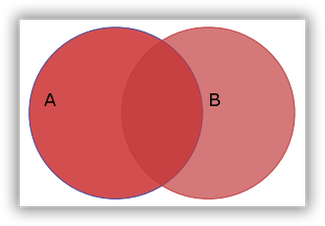
En la imagen la intersección es la parte obscura de la misma.
Ejemplo:
Sean A = {a, b, c, e, f}, B = {b, e, f, r, s} y
C = {a, t, u, v}.
Encuentre:
$A\cap B, A\cap C\,\,y\,\,C\cap B$
Como la intersección está formada por los elementos comunes de ambos conjuntos, se tiene que:

Cuando dos conjuntos no tienen elementos en común como B y C en el ejemplo anterior, se denominan Conjuntos disjuntos.
DIFERENCIA DE CONJUNTOS
Dados dos conjuntos A y B, se llama DIFERENCIA al conjunto:

Luego A-B se llama complemento de B con respecto a A.

En el diagrama de Venn A-B está representado por la zona rayada.
Ejemplo:
Sean A = {a, b, c} y B = {b, c, d, e}. Entonces:
A – B = {a} y B – A = {d, e}.
Asimismo, se llama DIFERENCIA SIMÉTRICA entre A y B al conjunto

En el diagrama de Venn la diferencia simétrica está representada por las regiones menos oscuras. (Lo que no tienen en común).
Ejemplo:
Sean A = {a, b, c, d} y B = {a, c, e, f, g}.
Entonces $A\bigtriangleup B=\left\{ b, d, e, f, g \right\} $
COMPLEMENTO DE UN CONJUNTO
Si un conjunto A es subconjunto de otro conjunto universal U, al conjunto A ' formado por todos los elementos de U, pero no de A, se llama complemento de A con respecto a U. Simbólicamente se expresa:


Ejemplos:
a) Sean U = {m, a, r, t, e } y A = {a, e }
Su complemento de A es: A' = {m, t, r}
b) Sean U = {letras de la palabra aritmética} y A = { e, i, a }
Determinado por extensión tenemos
U = {a, r, i, t, m, e, c} A = { e, i, a }
Su complemento es: A' = {r, t, m, c}

En forma gráfica:
PROPIEDADES DE LAS OPERACIONES BOOLEANAS
Las llamadas OPERACIONES BOOLEANAS (unión e intersección) verifican las siguientes propiedades:
Estas propiedades hacen que partes de U con las operaciones unión e intersección tenga una estructura de álgebra de Boole.
Además de éstas, se verifican también las siguientes propiedades:


PROBLEMAS CON OPERACIONES CON CONJUNTOS
Mediante diagramas de Venn y las definiciones y aplicación de las distintas operaciones con conjuntos se pueden resolver problemas, que nos preparan en el campo de la lógica formal.
Ejemplo:
A una fiesta llegaron 150 personas, de las cuales 75 cantan, 85 bailan, 20 no cantan ni bailan. ¿Cuántas personas cantan y bailan?
Solución: La pregunta lleva implícita una conectiva lógica y, que es parte importante de la definición formal de la operación intersección. Por lo tanto, podemos representar el problema de la siguiente manera:

Ejercicios:


4. En una encuesta realizada a 150 personas sobre sus preferencias de tres productos A, B y C, se encontró el siguiente resultado:
a. 82 consumen el producto A
b. 54 consumen el producto B
c. 50 sólo consumen el producto A
d. 30 sólo consumen el producto B
e. El número de personas que consumen sólo B y C es la mitad de las personas que consumen sólo A y C
f. El número de personas que consumen sólo A y B es el triple de las personas que consumen los tres productos
g. El número de personas que no consumen los productos mencionados son tantos como los que consumen sólo C
Determinar
a. El número de personas que consumen sólo dos de los productos
b. El número de personas que no consumen A, B ni C
c. El número de personas que por lo menos consumen uno de los productos


