La Divina Proporción

El número áureo o de oro (también llamado razón extrema y media, razón áurea, razón dorada, media áurea, proporción áurea y divina proporción) que usualmente se ha representado por la letra griega φ (fi) (en minúscula) o Φ (fi) (en mayúscula), en honor al escultor griego Fidias, es un número irracional, recordemos del noveno año, si mal no recuerdo, que un número irracional es aquel que no puede ser escrito como una razón, en términos más simples, no puede ser escrito como una fracción. Tal como lo podemos ver a continuación, se trata de un número algebraico irracional (decimal infinito no periódico). Así

\[\varphi = \frac{1+\sqrt{5}}{2}= 1,618033988749....\]

El mismo fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción entre segmentos de rectas. Esta proporción se encuentra tanto en algunas figuras geométricas como en la naturaleza. Puede hallarse en elementos geométricos, en las nervaduras de las hojas de algunos árboles, en el grosor de las ramas, en el caparazón de un caracol, en los flósculos de los girasoles, como vemos y si estás siguiendo las lecturas de esta web, el mismo está asociado a la maravillosa relación establecida por Dios creador del universo, de la matemática y la naturaleza y adoptada posteriormente por los geómetras griegos en la arquitectura y más adelante por connotados artistas del renacimiento.

A partir de algunas obras maravillosas se le ha atribuido un carácter estético a los objetos cuyas medidas guardan la proporción áurea. Considerándose incluso que posee una importancia mística.

El primero en hacer un estudio formal del número áureo fue Euclides (c. 300-265 a. C.), quién lo definió de la siguiente manera:

"Se dice que una recta ha sido cortada en extrema y media razón cuando la recta entera es al segmento mayor como el segmento mayor es al segmento menor."

Euclides Los Elementos Definición 3 del Libro Sexto.

Euclides demostró también que este número no puede ser descrito como la razón de dos números enteros, es decir, es un número irracional.

Filosofía y el número áureo

La pregunta filosófica que sugiere esto es ¿por qué esta proporción aparece con tanta frecuencia en la naturaleza? Principalmente se han propuesto tres respuestas:   

Respuesta teológica:según esta teoría el número áureo es una de las proporciones con las que Dios ha creado en universo. La reiteración de esta proporción en objetos naturales tan disimiles como una caracola y una piña, demuestra que el cosmos es fruto de una mente ordenadora y no del caos. Por esta razón muchos llaman a PHI proporción divina.

Respuesta naturalista: el número PHI es una secuencia fácil de reproducir por los seres naturales. Del mismo modo que en el desarrollo del feto de los mamíferos se produce una cuasi simetría entre las partes izquierda y derecha, en los objetos naturales se reproducen pautas sencillas y repetitivas antes que pautas azarosas. Téngase en cuenta que teniendo dos segmentos en proporción áurea podemos reproducir esta relación hasta el infinito de una manera meramente mecánica, por lo tanto, es natural que en el crecimiento animal y vegetal se reproduzca esta proporción.

Respuesta gnoseológica: desde una perspectiva kantiana asumimos que el espacio y el tiempo son formas a priori de nuestra sensibilidad. Son estructuras subjetivas que nos permiten acceder al conocimiento del mundo. Las matemáticas son fruto del autoexamen que hace el hombre de las propiedades de estas formas a priori de la sensibilidad: del espacio nace la geometría y del tiempo el álgebra. El número PHI no aparece, entonces, como fruto de Dios o de la naturaleza ciega, sino que aparece como una forma que tiene nuestra mente de captar o procesar el mundo externo. Una forma geométrica regular que imponemos al mundo cuando lo estructuramos en el acto cognitivo.

Tenemos entonces que cada quien, según su particular forma de pensar tendrá una respuesta. La última es la más filosófica de todas y en la que se deben admitir menos supuestos. Para un religioso la primera respuesta será la acertada, para un científico, seguro que la segunda.

Desde mi perspectiva ética y con la madurez de mis años, respetando todas las etapas por las que pasamos a lo largo de la misma, me llama la atención el planteamiento que en el año 1509 el matemático y teólogo Luca Pacioli publica en su libro De Divina Proportione (La Divina Proporción), en el que plantea cinco razones por las que estima apropiado considerar divino al Número áureo:

1.  «Es una y nada más que una». Pacioli compara el valor único de la Proporción Áurea al hecho de que la unidad «es el epíteto supremo de Dios».
2. Pacioli encuentra una similitud entre el hecho de que la definición de la Proporción Áurea comprenda tres longitudes de segmentos de recta y la existencia de la Santísima Trinidad: Padre, Hijo y Espíritu Santo.
3. Para Pacioli, la inconmensurabilidad de Dios y el hecho de que la Proporción Áurea sea un número irracional son equivalentes. En palabras suyas: «Del mismo modo que Dios no puede ser definido ni comprendido con palabras, nuestra proporción no puede designarse con números inteligibles ni expresarse con ninguna cantidad racional, sino que ha de permanecer escondida y en secreto, y es denominada irracional por los matemáticos».
4. Pacioli compara la omnipresencia y la invariabilidad de Dios con la auto-similitud asociada a la Proporción Áurea, es decir, el valor es siempre el mismo y no depende de que se divida la longitud de la línea o del tamaño del pentágono en que se calculen las proporciones de las longitudes.
5. En la quinta razón Pacioli afirma que, del mismo modo que Dios creó todo el cosmos a través de la quinta esencia, representada por el dodecaedro, la Proporción Áurea crea el dodecaedro, ya que no puede construirse sin la Proporción Áurea. Añade que sin la Proporción Áurea es imposible comparar los otros cuatro sólidos platónicos (que representan la tierra, el agua, el aire y el fuego) entre sí.

En el mismo libro, Pacioli no deja de ponderar las propiedades de la Proporción Áurea. Analiza, uno detrás de otro, lo que llama los trece «efectos» diferentes de la «Proporción Divina», calificando cada uno de estos «efectos» con adjetivos como «esencial», «singular», «maravilloso», «supremo», entre otros. Finalmente Pacioli se detiene en el «efecto» número trece, al concluir que «la lista debe finalizar, por la salvación», ya que había trece hombres sentados en la mesa de La Última Cena.

El astrónomo Johannes Kepler (1571-1630), desarrolló un modelo Platónico del Sistema Solar, y se refirió al número áureo en términos grandiosos...

“La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras; el otro, la división de una línea entre el extremo y su proporcional. El primero lo podemos comparar a una medida de oro; el segundo lo debemos denominar una joya preciosa”

Johannes Kepler en Mysterium Cosmographicum (El Misterio Cósmico).

El número áureo en las matemáticas

 Algunas expresiones matemáticas referentes al número áureo son, entre otras:

 
Ángulo de oro

\[\frac{360^{0}}{\varphi +1}\approx 137,5^0\]

Propiedades algebraicas

El número aúreo es la solución positiva para la siguiente ecuación cuadrática:

De la igualdad (1), tenemos que es el único número real positivo tal que:

\[\varphi ^2=\varphi +1\]

La expresión anterior, por ilógicamente matemática que parezca, es fácil de comprobar (una fórmula notable, aritmética simple y listo):

\[\begin{align*} \varphi ^2&=\left ( \frac{1+\sqrt{5}}{2} \right )^2=\frac{\left ( 1+\sqrt{5} \right )^2}{2^2}=\frac{1+2\sqrt{5}+\left ( \sqrt{5} \right )^2}{4}\\ &=\frac{1+2\sqrt{5}+5}{4}= \frac{6+2\sqrt{5}}{4}=\frac{3+\sqrt 5}{2} \end{align*}\]

Luego:

\[\varphi +1=\frac{1+\sqrt 5}{2}+1=\frac{1+\sqrt 5+2}{2}=\frac{3+\sqrt 5}{2}\]

Mágico, no… Vemos que las igualdades (1) y (2) nos muestran que tanto el cuadrado del número aúreo como su inverso conservan la misma parte decimal.

Porqué, los profesores de matemática no nos acercamos más a la naturaleza para enseñar esta bella ciencia, así lo hicieron los griegos, sin calculadoras y sin computadoras.

El número áureo posee además las siguientes propiedades:

\[\begin{align*}\varphi -1&=\frac{1}{\varphi} \\ \varphi^3&=\frac{\varphi+1}{\varphi-1} \end{align*}\]

Compruébalas por favor.

Para los informáticos, hablando de recurrencia tenemos que las potencias del número áureo pueden expresarse en función de una suma de potencias de grados inferiores del mismo número, establecida una verdadera sucesión recurrente de potencias.

El caso más simple es:

\[\varphi ^n=\varphi ^{n-1}+\varphi ^{n-2}\]

cualquiera sea n un número entero. Este caso es una sucesión recurrente de orden k = 2, pues se recurre a dos potencias anteriores.

Una ecuación recurrente de orden k tiene la forma:

\[a_1u_{n+k-1}+a_2u_{n+k-2}+.....+a_ku_n\]

En resumen: cualquier potencia del número áureo puede ser considerada como el elemento de una sucesión recurrente de órdenes 2, 4, 6, 8,..., 2k; donde k es un número natural. En la fórmula recurrente es posible que aparezcan potencias negativas de phi, hecho totalmente correcto. Además, una potencia negativa de phi corresponde a una potencia positiva de su inverso, la sección áurea.

Este curioso conjunto de propiedades y el hecho de que los coeficientes significativos sean los del binomio, parecieran indicar que entre el número áureo y el número e hay un parentesco.

Relación con la serie de Fibonacci

Si se denota el enésimo número de Fibonacci como Fn, y al siguiente número de Fibonacci, como Fn + 1, descubrimos que, a medida que n aumenta, esta razón oscila, y es alternativamente menor y mayor que la razón áurea. Podemos también notar que la fracción continua que describe al número áureo produce siempre números de Fibonacci a medida que aumenta el número de unos en la fracción.

Esta propiedad fue descubierta por el astrónomo alemán Johannes Kepler, pero pasaron más de cien años antes de que fuera demostrada por el matemático inglés Robert Simpson.

Con posterioridad se encontró que cualquier sucesión aditiva recurrente de orden 2 tiende al mismo límite. Por ejemplo, si tomamos dos números naturales arbitrarios, por ejemplo 3 y 7, la sucesión recurrente resulta: 3 - 7 - 10 - 17 - 27 - 44 - 71 - 115 - 186 - 301... Los cocientes de términos sucesivos producen aproximaciones racionales que se acercan asintóticamente por exceso y por defecto al mismo límite: 44/27 = 1,6296296...; 71/44 = 1,613636...; 301/186 = 1,6182795.

El número áureo en la geometría

El número áureo y la sección áurea están presentes en todos los objetos geométricos regulares o semirregulares en los que haya simetría pentagonal, que sean pentágonos o que aparezca de alguna manera la raíz cuadrada de cinco.

Relaciones entre las partes del pentágono.

Relaciones entre las partes del pentágono estrellado, pentáculo o pentagrama.

Relaciones entre las partes del decágono.

Relaciones entre las partes del dodecaedro y del icosaedro.

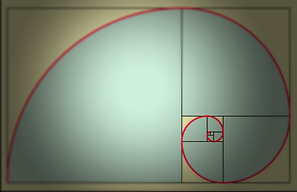
El rectángulo áureo de Euclides

El número áureo tiene un papel muy importante en los pentágonos regulares y en los pentagramas. Cada intersección de partes de un segmento interseca a otro segmento en una razón áurea.

El pentagrama incluye diez triángulos isóceles: cinco acutángulos y cinco obtusángulos. En ambos, la razón de lado mayor y el menor es φ. Estos triángulos se conocen como los triángulos áureos.

Teniendo en cuenta la gran simetría de este símbolo, se observa que dentro del pentágono interior es posible dibujar una nueva estrella, con una recursividad hasta el infinito. Del mismo modo, es posible dibujar un pentágono por el exterior, que sería a su vez el pentágono interior de una estrella más grande. Al medir la longitud total de una de las cinco líneas del pentáculo interior, resulta igual a la longitud de cualquiera de los brazos de la estrella mayor, o sea Φ. Por lo tanto, el número de veces en que aparece el número áureo en el pentagrama es infinito al anidar infinitos pentagramas.

El número áureo en la Naturaleza

Concha de nautilus en espiral logarítmica.

En la naturaleza, hay muchos elementos relacionados con la sección áurea y/o los números de Fibonacci:

La distribución de las hojas en un tallo. Ver: Sucesión de Fibonacci.

La relación entre las nervaduras de las hojas de los árboles

La relación entre el grosor de las ramas principales y el tronco, o entre las ramas principales y las secundarias (el grosor de una equivale a Φ tomando como unidad la rama superior).

La cantidad de espirales de una piña (ocho y trece espirales), flores o inflorescencias. Estos números son elementos de la sucesión de Fibonacci y el cociente de dos elementos consecutivos tiende al número áureo.

La cantidad de pétalos en las flores. Existen flores con 3, 5 y 8 pétalos y también con 13, 21, 34, 55, 89 y 144.

En la cantidad de elementos constituyentes de las espirales o dobles espirales de las inflorescencias, como en el caso del girasol, y en otros objetos orgánicos como las piñas de los pinos se encuentran números pertenecientes a la sucesión de Fibonacci. El cociente de dos números sucesivos de esta sucesión tiende al número áureo.

El número áureo en el arte y en la cultura

Relaciones en la forma de la Gran Pirámide de Gizeh.

La relación entre las partes, el techo y las columnas del Partenón, en Atenas (s. V a. C.).

En el cuadro Leda atómica, de Salvador Dalí, hecho en colaboración con el matemático rumano Matila Ghyka.

En los violines, la ubicación de las efes o eses (los “oídos” u orificios en la tapa) se relaciona con el número áureo.

El número áureo aparece en las relaciones entre altura y ancho de los objetos y personas que aparecen en las obras de Miguel Ángel, Durero y Leonardo Da Vinci, entre otros.

En las estructuras formales de las sonatas de Wolfgang Amadeus Mozart, en la Quinta Sinfonía de Ludwig van Beethoven, en obras de Franz Schubert y Claude Debussy (estos compositores probablemente compusieron estas relaciones de manera inconsciente, basándose en equilibrios de masas sonoras).

El número phi aparece en la película de Disney "Donald en el país de las matemáticas".