Ángulos

Un ángulo es la abertura comprendida entre dos rayos o semirrectas con un punto común denominado vértice.

El ángulo puede denotarse de cualquiera de las siguientes formas:

\[\angle ABC \thinspace o \thinspace \angle \alpha \thinspace o \thinspace\widehat{ABC} \thinspace o \thinspace \widehat{\alpha}\]

Medición de ángulos
Los ángulos se miden en grados o en radianes. El sistema usualmente usado es en grados sexagesimales y se miden en el sentido contrario a las manecillas del reloj analógico.

El sistema sexagesimal consiste en dividir la circunferencia en 360 partes iguales llamadas grados, estos a su vez se dividen en 60 partes iguales denominadas minutos y los minutos se dividen en sesenta partes iguales que se denominan segundos.

Construcción de un ángulo
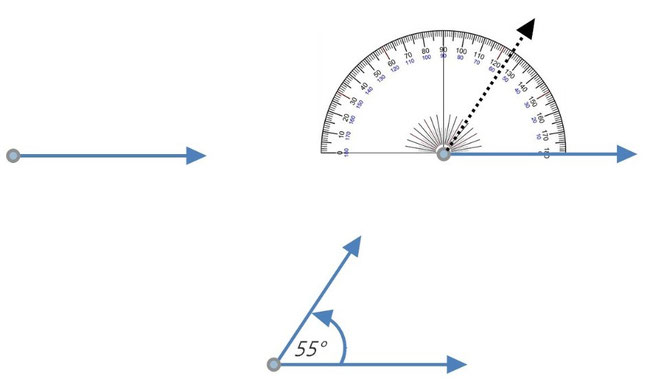
Para construir un ángulo con regla y compás:

1) trazas el lado inicial sobre el cual colocarás el transportador haciendo coincidir el vértice con el punto correspondiente en el compás y,

2) luego marcas según la medida requerida. Sigue paso a paso según la ilustración.

Clasificación de los ángulos según su medida
Los ángulos se clasifican según su medida tal como se indica a continuación:

Agudo:
Es un ángulo tal que su medida está limitada por el intervalo comprendido entre 0° y 90°.

\[0° < m\angle \beta < 90°\]

Recto:
Es un ángulo tal que su medida es 90°.

\[m\angle \beta = 90°\]

Obtuso:
Es un ángulo tal que su medida está limitada por el intervalo comprendido entre 90° y 180°.

\[90° < m\angle \beta < 180°\]

Llano:

Es todo aquel ángulo tal que su medida es igual a 180°.

\[m\angle \beta = 180°\]

Nulo:

Ángulo cuya medida es igual a 0°.

\[m\angle \beta = 0°\]

Cóncavo:

Es el ángulo cuya medida está en el intervalo comprendido entre 180° y 360°.

\[180° < m\angle \beta < 360°\]

Clasificación de los ángulos por la suma de sus medidas

Los ángulos adyacentes reciben distintos nombres si la suma de sus medidas es 90°, 180° o 360°, tal como mostramos a continuación.

Ángulos complementarios

Dos ángulos adyacentes se llaman complementarios si la suma de sus medidas es igual a 90°. Los ángulos A y B son ángulos complementarios.

\[m\angle A + m\angle B = 90°\]

Ángulos suplementarios

Dos ángulos adyacentes se llaman suplementarios si la suma de sus medidas es igual a 180°. Los ángulos I y K son ángulos suplementarios.

\[m\angle K + m\angle I = 180°\]

Ángulos conjugados

Dos ángulos adyacentes se llaman conjugados si la suma de sus medidas es igual a 360°. Los ángulos L y M son ángulos conjugados.

\[m\angle L + m\angle M = 360°\]

Ejemplos:

Determinar el valor de cada ángulo en la siguiente figura siendo AB y AC perpendiculares.

Solución:
Los ángulos BAD y DAC son complementarios por ser ángulos contiguos y cuya suma es 90°.

Por lo tanto:

\[\begin{align*} 2x - 20 + x - 10 &= 90 \\ 3x - 30 &= 90 \\ 3x &= 120 \\ x &= 40° \end{align*}\]

R./ La medida del ángulo BAD es (2*40 – 20) = 60° y,
la medida del ángulo DAC es (40-10)=30°

2. Encuentre el valor de los ángulos de la siguiente figura.

Solución:

Los ángulos GEI, IEH y HEF son suplementarios por ser ángulos adyacentes y cuya suma es 180°.

Por lo tanto tenemos que:

\[\begin{align*} \left (x - 10° \right )+ 3x + \left ( 2x - 20° \right ) &= 180° \\ 6x - 30° &= 180° \\ 6x &= 210° \\ x &= 35° \end{align*}\]

R./ La medida del ángulo GEI es (2*35)-20 = 50°,
La medida del ángulo IEH es (3*35)= 105° y,
La medida del ángulo HEF es (35 – 10) = 25°.

Clasificación de los ángulos según sus lados

Observemos la figura determinada por la intersección de dos rectas y los ángulos que se obtienen de esa intersección.

Los ángulos que tienen la misma medida se denominan ángulos opuestos por el vértice. En la figura los pares de ángulos a y b y c y d son ángulos opuestos por el vértice.

Los ángulos que tienen un lado común y están ambos sobre la misma recta se denominan ángulos adyacentes.

En la figura los pares de ángulos a y c y b y d son ángulos adyacentes.

Observando la figura ¿qué podemos concluir con relación a los ángulos adyacentes?

Ángulos formados por dos rectas secantes o dos paralelas cortadas por una transversal

En la figura adyacente se tienen ocho ángulos, los clasificaremos en pares para obtener algunas relaciones importantes entre ellos.

Ángulos correspondientes
Los siguientes pares de ángulos se llaman correspondientes.

Cada par de ángulos correspondientes son congruentes entre sí, i.e. tienen la misma medida.

Ángulos Alternos Internos
Los siguientes pares de ángulos se llaman ángulos alternos internos

Teorema
Cada par de ángulos alternos internos, situados a uno y otro lado de la transversal que es lado común, son congruentes entre sí.

Demostración:

Se tiene que las rectas JK y LM son paralelas cortadas por una transversal.

Demostrar que los ángulos B y D son congruentes.

\[\begin{align*} \angle B &\cong \angle D \hspace{4cm} \hfill Por\ ser\ opuestos\ por\ el\ vértice \hfill\\ \angle B & \cong \angle F \hspace{4cm} \hfill Porque\ son\ correspondientes \hfill \\ \therefore \angle D &\cong \angle F \hspace{4cm} \hfill Por\ transitividad. \end{align*}\]

Ángulos alternos externos
Los siguientes pares de ángulos se llaman ángulos alternos externos.

Teorema
Cada par de ángulos alternos externos, situados a uno y otro lado de la transversal que es lado común, son congruentes entre sí.

Demostración:

Se tiene que las rectas JK y LM son paralelas cortadas por una transversal.
Demostrar que los ángulos A y B son congruentes.

\[\begin{align*} \angle B &\cong \angle P \hspace{4cm} \hfill Por\ ser\ opuestos\ por\ el\ vértice \hfill\\ \angle A & \cong \angle P \hspace{4cm} \hfill Porque\ son\ correspondientes \hfill \\ \therefore \angle A &\cong \angle D \hspace{4cm} \hfill Por\ transitividad. \end{align*}\]

Ejemplos
1. Calcular el valor en cada uno de los siguientes ángulos.

Solución:

Los ángulos 2x y x forman un par lineal es decir son ángulos suplementarios, por lo tanto:

\[\begin{align*} 2x + x &= 180° \\ 3x &= 180° \\ x &= 60° \end{align*}\]

\[\begin{align*} \angle \alpha &\cong \angle x \hspace{2cm} \hfill Por\ ser\ opuestos\ por\ el\ vértice\ \hfill \\ m \angle \alpha + m \angle \beta &= 180° \hspace{2cm} \hfill Porque\ son\ suplementarios\ \hfill \\ \end{align*}\]

\[\begin{align*} \therefore m \angle \alpha &= 60° \\ m \angle \beta &= 120° \\ m \angle 2x &= 120° \end{align*}\]

2. Si K y L son rectas paralelas cortadas por una transversal obtener el valor de los ángulos indicados.

Solución:

Los ángulos a y 3x + 6 son suplementarios.
Los ángulos 3x + 6 y e son correspondientes por lo que son ángulos congruentes.
Los ángulos d y x son congruentes por ser opuestos por el vértice
Los ángulos a y d son congruentes por ser correspondientes.

Por transitividad el ángulo a es congruente al ángulo x.

Tenemos que:

\[\begin{align*} x+3x+6 &=180\\ 4x &= 180 - 6\\ x &= \frac{172}{4} \\ x &= 43,5° = 43° 30' \end{align*}\]

Los ángulos a, d y x miden 43° 30’,
luego 3x + 6 = 3*43,5+6=136,5°= 136° 30’, por lo tanto:
Los ángulos 3x + 6, b y e miden 136° 30’

Ejercicios
1. Si el complemento de un ángulo es el doble. ¿Cuál es la medida en grados de cada ángulo?

2. Si el suplemento de un ángulo es un tercio del ángulo X. ¿Cuál es la medida de cada ángulo?

3. Determinar la medida de dos ángulos A y B tales que son complementarios y su diferencia es 10°.

4. Halla la medida de dos ángulos suplementarios tal que uno es 20° mayor que el otro.

5. En cada caso obtener el valor del ángulo desconocido, justifique su respuesta.

Siguiente tema Triángulos