Teorema de Thales

Teorema: Si varias rectas paralelas cortan a dos transversales, entonces los segmentos que determinan las paralelas en una de las transversales, son proporcionales a los segmentos correspondientes de la otra transversal.

\[\frac{\overline{JL}}{\overline{KM}}= \frac{\overline{LN}}{\overline{MO}}=\frac{\overline{JN}}{\overline{KO}}\]

Ejemplo:
Las rectas de la figura MN, KL e IJ son paralelas, hallar la longitud de x.

Solución

\[\begin{align*} \frac{\overline{IK}}{\overline{JL}}&=\frac{\overline{KM}}{\overline{LN}} \\ \frac{16}{x} &= \frac{20}{22}\\ 16 \cdot 22 &= 20x \\ x &= \frac{16 \cdot 22}{20} \\ x &= \frac{352}{20} \\ x &= 17,6 \end{align*}\]

R/. El valor del segmento JL es de 17,6 unidades de distancia.

El teorema de Thales en un triángulo
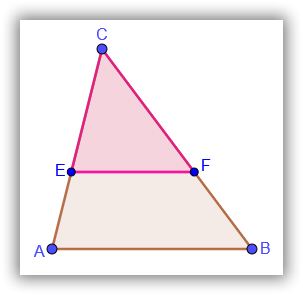
Dado un triángulo ABC, si se traza un segmento paralelo, EF, a uno de los lados del triangulo, se obtiene otro triángulo CEF, cuyos lados son proporcionales a los del triángulo ABC.

\[\frac{\overline{AC}}{\overline{EC}}=\frac{\overline{BC}}{\overline{FC}}=\frac{\overline{AB}}{\overline{EF}}\]

Ejemplo:
Hallar la medida de x, de acuerdo a los datos suministrados en la figura.
Solución:

\[\begin{align*} \frac{\overline{DC}}{\overline{AD}}&=\frac{\overline{EC}}{\overline{BE}} \\ \frac{16}{28} &= \frac{18}{x}\\ 16x &= 28 \cdot 18 \\ x &= \frac{28 \cdot 18}{16} \\ x &= \frac{504}{16} \\ x &= 31,5 \end{align*}\]

R/. La medida del segmento x es de 31,5 unidades de longitud.

Ejercicios:
1. Calcular el valor del lado o lados desconocidos en las siguientes figuras, siendo que AB es paralela a DE.

2. En algún momento del día un edificio de 55m de altura proyecta una sombra de 24 m. ¿Cuál es la longitud de la sombra proyectada por un semáforo de 4,5 m de altura?

3. Para medir la longitud de un lago, se trazan las siguientes medidas correspondientes a triángulos semejantes. Si AB = 275m, AD = 115m y DC= 60m.

¿Cuál es la longitud del lago?

4. En cada caso calcular el valor de x.

5. Hallar el valor de x.

Siguiente tema: Teorema de Pitágoras