Homotecias
Transformaciones Geométricas

Una transformación geométrica es una operación que permite generar una nueva figura de la originalmente dada. La transformación se llama homólogo del original. En función del aspecto de la figura homóloga respecto de la original, las transformaciones pueden ser:
Isométricas: Cuando las figuras conservan sus dimensiones y medidas angulares. Entre ellas se tiene la simetría axial y central, las traslaciones y las rotaciones.
Isomorfas: Conservan la forma de la figura original. Existe proporcionalidad entre la figura original y su homóloga.
Una homotecia es una transformación geométrica isomorfa en el plano donde, a partir de un punto fijo llamado centro de homotecia (O), y un factor de escala se obtiene una o más figuras llamadas homotéticas.
De esta forma, cada punto A corresponde a otro punto A' producto de la transformación, y estos se encuentran perfectamente alineados con el centro de homotecia O.
La homotecia es una transformación que puede generar imágenes congruentes si el factor de escala es 1 o -1, mientras que para valores distintos a 1 o -1, la figura original generará una o más figuras semejantes de mayor o menor tamaño; es decir, la homotecia transforma un polígono en otro semejante.
En cualquier homotecia se establece una correspondencia punto a punto, recta a recta y ángulo a ángulo, de forma que las parejas de puntos homólogos estén alineadas con el centro de homotecia. De igual forma, las parejas de segmentos que los unen deben ser paralelas y los ángulos homólogos o correspondientes son congruentes. La relación entre tales segmentos es una constante llamada razón de la homotecia (k); de tal forma que la homotecia puede ser definida como:
Para hacer este tipo de transformación se dibuja un polígono cualquiera y luego se escoge un punto arbitrario, que será el centro de la homotecia.
A partir de este punto se trazan segmentos de recta para cada vértice de la figura que se va a transformar. La escala en la que se hace la reproducción de la nueva figura es dada por la razón de la homotecia (k).
Propiedades
Una de las principales propiedades de la homotecia es que, por la razón de la homotecia (k), todas las figuras homotéticas son semejantes. Entre otras propiedades destacadas se encuentran las siguientes:
– El centro de la homotecia (O) es el único punto que se transforma en sí mismo; es decir, no varía.
– Las rectas que pasan por el centro se transforman en sí mismas (son dobles), pero los puntos que las componen no son dobles.
– Las rectas que no pasan por el centro se transforman en rectas paralelas; de esa forma, los ángulos de la homotecia son congruentes.
– La imagen de un segmento por una homotecia de centro O y razón k, es un segmento paralelo a este y tiene k veces su longitud.
– Los ángulos homotéticos son congruentes; es decir, tienen la misma medida.
Por otra parte, se tiene que la homotecia varía en función del valor de su razón (k), y pueden ocurrir los siguientes casos:
– Si la constante k = 1, todos los puntos son fijos porque se transforman a sí mismos. Así, la figura homotética coincide con la original y la trasformación se llamará función identidad.
– Si k ≠ 1, el único punto fijo será el centro de la homotecia (O).
– Si k = -1, la homotecia se convierte en una simetría central (C); es decir, ocurrirá una rotación alrededor de C, en un ángulo de 180°.
Clasificación
Las homotecias también pueden ser clasificadas en dos tipos, en función del valor del valor de la razón (k):
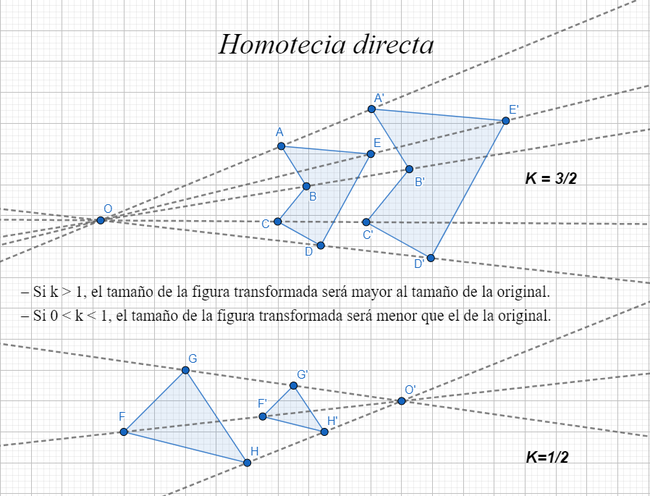
Homotecia directa
Ocurre si la constante k > 0; en este caso, los puntos homotéticos se encuentran al mismo lado con respecto al centro:
El factor de proporcionalidad o razón de semejanza entre las figuras homotéticas directas siempre será positivo.
Homotecia inversa
Ocurre si la constante k < 0; es decir, los puntos iniciales y sus homotéticos se ubican en los extremos opuestos con respecto al centro de la homotecia pero alineados a esta. El centro se encontrará entre las dos figuras:
El factor de proporcionalidad o razón de semejanza entre las figuras homotéticas inversas siempre será negativo.
Producto de Homotecias
El producto de dos homotecias es otra homotecia, cuyo centro está alineado con los centros de las dos transformaciones originales (aunque esta homotecia final puede resultar de centro impropio, convirtiéndose en una traslación) y cuya razón es el producto de las dos razones.