Congruencia de triángulos

Definición: Dos o más triángulos se dice que son congruentes si tienen la misma forma y el mismo tamaño.

Si dos triángulos son congruentes entonces los lados correspondientes son iguales y los ángulos correspondientes son iguales. En geometría a los lados correspondientes se les suele llamar lados homólogos y a los ángulos correspondientes se les dice ángulos homólogos.

Los triángulos ABC y A’B’C’ son congruentes porque sus lados y ángulos correspondientes son iguales.

La expresión «El triángulo ABC es congruente al triángulo A’B’C’» se escribe así:

\[\Delta ABC \cong \Delta A'B'C'\]

Teoremas de congruencia de triángulos
Teorema 1 (L-L-L)

Dos triángulos son congruentes si tienen sus lados correspondientes iguales.

\[\begin{align*} \overline{AB} &\cong \overline{DE} \\ \overline{BC} &\cong \overline{EF} \\ \overline{AC} &\cong \overline{DF}\\ \therefore \Delta ABC &\cong \Delta DEF \end{align*}\]

Teorema 2 (A-L-A)

Dos triángulos son congruentes si tienen dos ángulos correspondientes iguales y el lado común adyacente a ellos también es igual.

\[\begin{align*} \angle \alpha & \cong\angle \gamma \\ \overline{BC} &\cong \overline{EF} \\ \angle \beta &\cong \angle \delta\\ \therefore \Delta ABC &\cong \Delta DEF \end{align*}\]

Teorema 3 (L-A-L)

Dos triángulos son congruentes si dos lados correspondientes y el ángulo comprendido entre ellos son iguales.

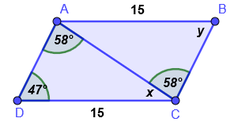
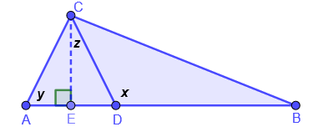
\[\begin{align*} \overline{AB} &\cong \overline{DE} \\ \angle \beta & \cong\angle \varepsilon \\ \overline{BC} &\cong \overline{EF} \\ \therefore \Delta ABC &\cong \Delta DEF \end{align*}\]

Ejemplo 1.

En la figura AB es paralela a DC. Determine si los triángulos son congruentes y cuales son los valores de los ángulos x, y.

Solución:

Afirmaciones

Justificaciones

\[\begin{align*} \overline{AB} &\cong \overline{DC} & &Datos \\ \angle DAC &\cong \angle BCA & &Datos \\ \overline{AC} &\cong \overline{CA} & &Datos\ lado\ común\ \\ \angle y &= 47° & &Por\ ser\ homólogo\ al\ ángulo\ ADC\ \\ \angle x &= 75° & &La\ suma\ de\ los\ ángulos\ internos\ del\ triángulo\ \\ \angle CAB &= 75° & &Alternos\ internos\ entre\ paralelas\ \\ \Delta ADC &\cong \Delta CBA & &Teorema\ A-L-A\ \end{align*}\]

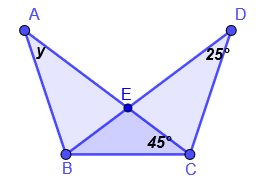
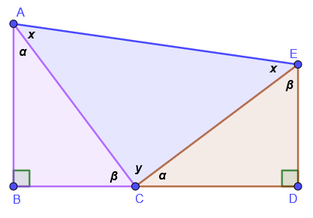
Ejemplo 2.

En la figura AB es bisectriz del ángulo CAD, AC es congruente al segmento AD. Demuestre que AB también es bisectriz del ángulo CBD.

Solución:

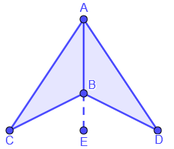
Afirmaciones

Justificaciones

\begin{align*} \angle CAB & \cong\angle DAB & &Datos\ Recta\ \overline{AB}\ biseca\ \angle CAD \\ \overline{AC} &\cong \overline{AD} & &Datos\\ \overline{AB} &\cong \overline{BA} & &Datos\ (por\ ser\ lado\ común)\\ \Delta ABC &\cong \Delta ABD & &Por\ Teorema\ L-A-L \\ \angle ABC &\cong\angle ABD & &Por\ ser\ homólogos\\ \angle CBE & \cong\angle DBE & & \angle ABC+\angle CBE = \angle ABD+\angle DBE \end{align*}

Por lo tanto el segmento AE biseca al ángulo CBD.

Ejercicios:

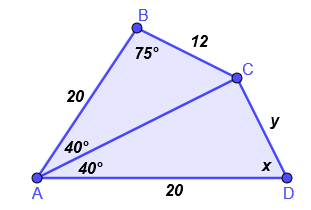
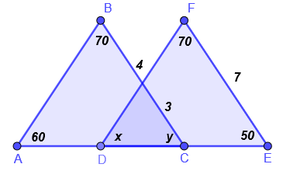
1. Determine el valor de x, y. Justifique si existe congruencia.

2. Determine el valor de x, y. Justifique si existe congruencia.

3. Calcular el valor de la incógnita y justifique la congruencia. Considere que además se cumple:

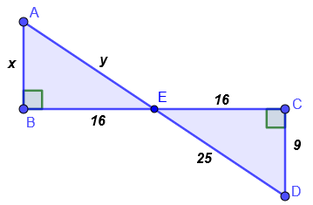
\[\begin{align*} \angle ABC & = 110° \\ \overline{AC} &\bot \overline{AD} \\ \end{align*}\]

4. Calcular los valores desconocidos. Justifique si existe congruencia entre triángulos. Considere que además se cumple que;

CD es bisectriz del ángulo ECB.

\[\begin{align*} \angle z & = 25° \\ \overline{CE} &\bot \overline{AD} \\ \end{align*}\]

5. Determinar el criterio de congruencia entre triángulos y calcular los valores desconocidos.

6. Calcule el valor del ángulo x. Indique si existe al menos un par de triángulos congruentes. Considere que:

\[\begin{align*} \overline{AB} &\cong \overline{CD} \\ \overline{BC} &\cong \overline{DE} \\ \end{align*}\]

Siguiente tema: Semejanza de triángulos