Notación
Definición: Una función f de un conjunto A a un conjunto B, es una correspondencia que asigna a cada elemento x de A un único elemento y del conjunto B.
Al conjunto A se le denomina dominio de la función y al conjunto B se le llama codominio de la función. El elemento y de B asociado al elemento x de A se le llama imagen de x bajo f y se denota f(x). El conjunto de los valores f(x) del codominio se denomina Rango de f y en este caso se representa f(A).
El gráfico de f, se denota Gf y es el conjunto de pares ordenados tales que el primer elemento de cada par ordenado es un elemento del dominio de f y el segundo elemento corresponde a su imagen y por lo tanto perteneciente al codominio de f.

Para indicar que f es una función de dominio A y codominio B se usa la siguiente notación:

La representación f(x) que corresponde a la imagen de x bajo la función f, es un elemento de B.

Ejemplos:
1. Considere la función f: A àB dada en el siguiente diagrama
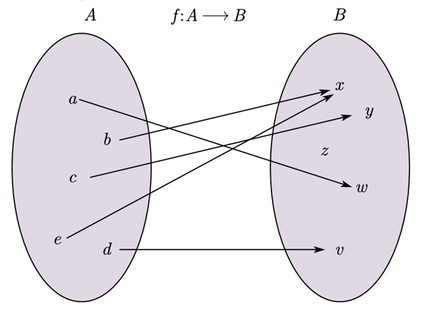
Del diagrama de la función f, podemos decir:
El dominio de f es A={a, b, c, d, e}
El codominio de f es B={x, y, z, w, v}
El rango de la función es R={x, y, w, v}
f(a) = w La imagen de a bajo f es w Una preimagen de w bajo f es a
f(b) = x La imagen de b bajo f es x Una preimagen de x bajo f es b
f(c) = y La imagen de c bajo f es y Una preimagen de y bajo f es c
f(d) = v La imagen de d bajo f es v Una preimagen de v bajo f es d
f(e) = x La imagen de e bajo f es x Una preimagen de x bajo f es e
El ámbito de la función es R={x, y, w, v}
El gráfico de la función f es Gf = {(a, w), (b, x), (c, y), (d, v), (e, x)}
2. Sea la función definida por

En tal caso f es una función con dominio {1, 2, 3, 4, 5} y codominio el conjunto de los números reales. Determinar el ámbito.

3. Sea f la relación definida por el siguiente diagrama. Analizar y escribir su conclusión

Por definición se sabe que una función f de un conjunto A a un conjunto B, es una correspondencia que asigna a cada elemento x de A un único elemento y del conjunto B. Como podemos ver a 8 no le corresponde ningún elemento del conjunto B, por lo tanto lo que muestra el diagrama no es una función.
4. Dada la siguiente relación, analice y escriba su conclusión.

Si analizamos la relación tenemos que:

Como vemos para x = 2, x = 3 y x = 5 no existe un número entero asociado a la raíz cuadrada de esos números. Por lo tanto la relación no es una función.
5. Para la gráfica dada a continuación concluya si la relación es una función.
La relación no es función ya que como podemos ver a 1 se le asocian dos valores diferentes: 2 y 3.
Definición: Una función f de A en B se llama función real de variable real si se cumple la siguiente condición:

Verifica tu aprendizaje
a) Para cada diagrama explica si representa una función.

b) Completa cada tabla a partir de la función dada.



