Funciones crecientes y decrecientes
Una función f es creciente en un intervalo si para cualquier par de valores x1 y x2 del intervalo:


Una función f es creciente en un intervalo si para cualquier par de valores x1 y x2 del intervalo:

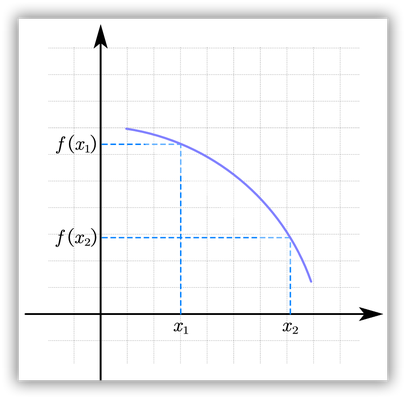
Ejemplos:
1. Observe la gráfica de la siguiente función
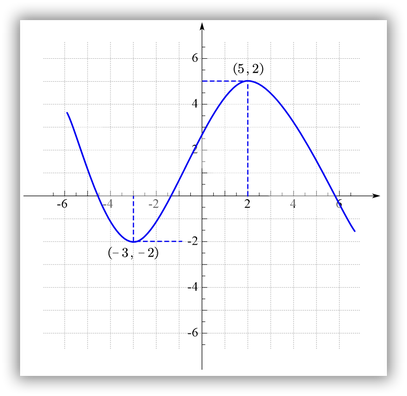
La función representada en la gráfica anterior tiene el siguiente comportamiento

2. Analice el gráfico de la función f y concluya

La función representada en la gráfica anterior tiene el siguiente comportamiento

Verifica tu aprendizaje
Para cada una de las funciones cuyas gráficas se dan a continuación, indique:
a) El dominio y el rango
b) El intervalo o intervalos donde la función es creciente
c) El intervalo o intervalos donde la función es decreciente

Función constante
Una función es constante en un intervalo si para cualquier par de puntos x1 y x2 del intervalo y tales que x1 < x2, se cumple que f(x1) = f(x2).
De otra forma una función es constante si al aumentar la variable independiente x, la variable dependiente y no varía.

También se puede analizar el crecimiento y decrecimiento de una función si esta es derivable.
Funciones crecientes y decrecientes y su relación con su derivada
Crecimiento y decrecimiento en un punto.
Si tenemos una función f, derivable en un punto a, entonces tenemos que:
La función f es creciente en el punto a si f’(a) > 0. Es decir es creciente en a si la derivada es positiva.

La función f es creciente en el punto a si f’(a) < 0. Es decir es creciente en a si la derivada es negativa.

La función f es constante en el punto a si f’(a) = 0. Es decir es constante en a si la derivada es igual a cero.

Ejemplos:
Analizar el crecimiento de la siguiente función en los puntos 0, 1 y 3.

Paso 1. Calculamos la derivada de f

Crecimiento y decrecimiento de una función en un intervalo
Si f es una función continua definida en un intervalo [a, b], la siguiente podría ser la representación gráfica de f en el intervalo previamente establecido.

En la gráfica anterior podemos observar que la función f tiene el siguiente comportamiento:
a) Creciente en los intervalos ]a, x1[ y ]x2, x3[
b) Decreciente en los intervalos ]x1, x2[ y ]x3, b[
También se puede ver que cuando la pendiente de la recta tangente a esos puntos es positiva, la función crece; y cuando la pendiente de la recta tangente es negativa la función decrece.
Además, si trazáramos una recta tangente en los puntos (x1, f(x1)) y (x3, f(x3)) obtendríamos una recta horizontal, paralela al eje X, por lo que su pendiente es cero.
Teorema:
Sea f una función continua en un intervalo cerrado [a, b] y derivable en el intervalo ]a, b[.
1. Si f’(x) > 0 para toda x en ]a, b[, entonces la función f es creciente en [a, b].
2. Si f’(x) < 0 para toda x en ]a, b[, entonces la función f es decreciente en [a, b].
Ejemplos:
1. Determinar los intervalos sobre los cuales la siguiente función es creciente o decreciente

Solución:
Paso 1. Derivamos f

Paso 2. Igualamos la primera derivada a cero, para determinar los puntos críticos

Paso 3. Construimos la tabla de variación
Se concluye que:


2. Determinar los intervalos sobre los cuales la siguiente función es creciente o decreciente

Solución:
Paso 1. Derivamos f

Paso 2. Igualamos la primera derivada a cero, para determinar los puntos críticos

Paso 3. Construimos la tabla de variación
Se concluye que:




