Una función se dice que es inyectiva si no hay dos o más elementos del dominio que tengan una misma imagen del codominio.

Ejemplos:

1.      La función f:AàB, definida en el siguiente diagrama es inyectiva porque los elementos del rango tienen a lo sumo una preimagen.

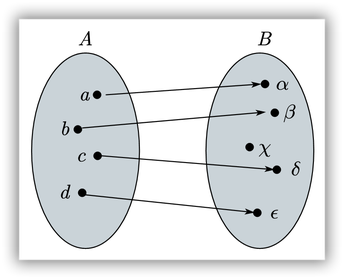
2.      La función f:AàB, definida en el siguiente diagrama NO es inyectiva porque al menos un elemento del rango tiene dos preimágenes.

3.      La función f:[a, b]àR de la gráfica es inyectiva puesto que no existe elemento alguno en el rango con más de una preimagen.

4.      La función f:[a, b]àR de la gráfica NO es inyectiva puesto que existen elementos en el rango con más de una preimagen.

Una función se dice que es sobreyectiva o suprayectiva cuando los elementos del codominio son los mismos elementos del rango o recorrido.

Ejemplos:

1.      Sea la función f:AàB, definida en el siguiente diagrama. Podemos ver que todo elemento del codominio B tiene al menos una preimagen en el conjunto A, por lo tanto concluimos que la función es sobreyectiva.

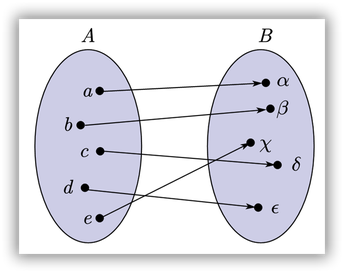
2.      Sea la función f:AàB, definida en el siguiente diagrama. Podemos ver que existe un elemento del codominio B que no tiene una preimagen en el conjunto A, por lo tanto concluimos que la función NO es sobreyectiva.

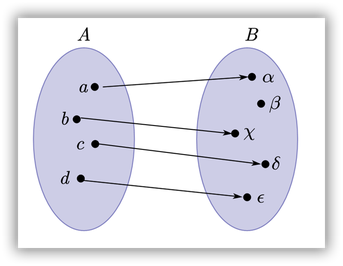
3.      La función f:[a, b]à[c, d] de la gráfica adjunta, ésta es sobreyectiva puesto que para cada elemento de [c, d] en el codominio existe al menos una preimagen en [a, b].

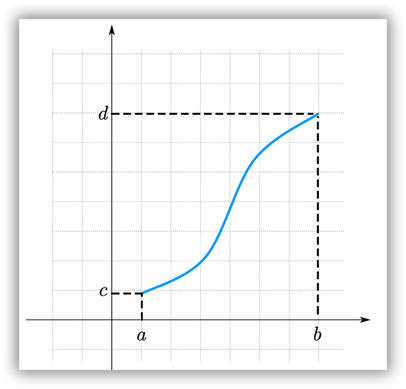
4.      La función real de variable real de la gráfica adjunta, no es sobreyectiva puesto que existen elementos en el dominio que NO tienen una imagen en el codominio.

5.      Considere la función definida de la siguiente manera:

Vemos que la expresión algebraica que define la función, se indefine para x = 0. En esta función cualquier valor x del codominio tiene preimagen, ya que para todo número real distinto de cero, existe su correspondiente inverso multiplicativo que es un número real, también diferente de cero.

Una función f es biyectiva si es inyectiva y sobreyectiva, es decir, todo elemento del codominio posee una única preimagen.

Ejemplos:

1.      La función real de variable real definida por f(x)=x+2 es biyectiva.

La función es inyectiva puesto que para cada número real del dominio existe un único número real en el codominio.

La función es sobreyectiva puesto que no existe elemento del codominio que no sea imagen.

2.      Sea la función real de variable real dada por la gráfica adjunta

La función no es inyectiva, ya que tenemos elementos del codominio que son imágenes de más de un elemento del dominio.  Se comprueba que si utilizamos la prueba de la línea horizontal, esta corta a la gráfica en más de un punto.

Por lo tanto, si la función NO es inyectiva, consecuentemente no es biyectiva.

Comprueba tu aprendizaje

Para cada función dada a continuación, determine si la función en cuestión es inyectiva, sobreyectiva, biyectiva o ninguna de estas.