Al trabajar con histogramas y polígonos de frecuencias, vimos que las distribución de los datos pueden adoptar varias formas. En algunas distribuciones los datos tienden a agruparse más en una parte de la distribución que en otra. Comenzaremos a analizar las distribuciones con el objeto de obtener medidas descriptivas numéricas llamadas estadísticas, que nos ayuden en el análisis de las características de los datos. Dos de estas características son de particular importancia para los responsables de tomar decisiones: la tendencia central y la dispersión.

Tendencia central: La tendencia central se refiere al punto medio de una distribución. Las medidas de tendencia central se denominan medidas de posición.

Ejemplo 1: Los siguientes datos representan la cantidad de pedidos diarios recibidos en un período de 20 días, ordenados en orden ascendente

0       0       1        1       2       2       4       4       5       5

6       6       7       7        8      12     15     15     15     19

                  Mo = 15        La cantidad de pedidos diarios que más se repite es 15

Ejemplo 2: La cantidad de errores de facturación por día en un período de 20 días, ordenados en orden ascendente es

Esta distribución tiene 2 modas. Se la llama distribución bimodal.

Mo = 1   y Mo = 4

Cálculo de la moda para datos agrupados

Si los datos están agrupados en una distribución de frecuencias, se selecciona el intervalo de clase que tiene mayor frecuencia llamado clase modal.

Para determinar un solo valor de este intervalo para la moda utilizamos la siguiente ecuación:

\[Mo=L_{i}+c\left ( \frac{d_{1}}{d_{1}+d_{2}} \right )\]

Donde:

Mo = Moda

L_i = Límite inferior real de la clase modal

c = Intervalo de la clase modal

d₁ = f_i – f_{i – 1} = diferencia entre las frecuencias de la clase modal y la premodal

d₂ = f_i – f_{i + 1} = diferencia entre las frecuencias de la clase modal y la postmodal

Ejemplo 3: La edad de los jubilados encuestados en el Área Metropolitana en noviembre del 2008

La clase modal es [60, 70), ya que es la que presenta la mayor frecuencia

\begin{align*} L_{i}&=60 &f_{i}&=18 &f_{i-1}&=10 &f_{i+1}&=14 &c&=10\\ d_{1}&=f_{i}-f_{i-1} &d_{2}&=f_{i}-f_{i+1}\\ d_{1}&=18-10 &d_{2}&=18-14\\ d_{1}&=8 &d_{2}&=4 \end{align*}

\begin{align*} Mo&=L_{i}+c\left ( \frac{d_{1}}{d_{1}+d_{2}} \right )\\ &=60+10\left ( \frac{8}{8+4} \right )\\ &=66,66 \end{align*}

VENTAJAS Y DESVENTAJAS DE LA MODA

• Se puede utilizar para datos cualitativos nominales u ordinales y para datos cuantitativos
• No se ve afectada por los valores extremos
• Se puede utilizar cuando la distribución de frecuencias tenga clases abiertas
• Cuando todas las puntuaciones de un grupo tienen la misma frecuencia, se dice que no tiene moda
• Si un conjunto de datos contiene 2 puntuaciones adyacentes con la misma frecuencia común (mayor quecualquier otra), la moda es el promedio de las 2 puntuaciones adyacentes Ej. (0,1,1,2,2,2,3,3,3,4,5) tiene Mo=2,5
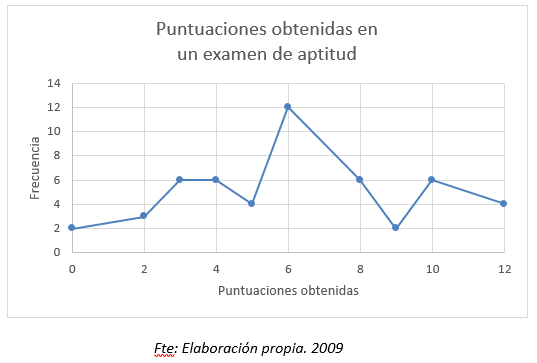
• Si en un conjunto de datos hay dos que no son adyacentes con la misma frecuencia mayor que las demás, es una distribución bimodal. Conjuntos muy numerosos se denominan bimodales cuando presentan un polígono de frecuencias con 2 lomos, aun cuando las frecuencias en los 2 picos no sean exactamente iguales. Estas ligeras distorsiones de la definición están permitidas porque el término bimodal es muy conveniente y en último término es descriptivo. Una distinción conveniente puede hacerse entre la moda mayor y la moda menor. Por ejemplo en el gráfico siguiente, la moda mayor es 6 y las menores son 3,5 y 10.