Regla de sustitución o de la cadena

El método de integración por sustitución se utiliza en aquellos casos en los que el diferencial a integrar, es producto de una función compuesta. En tales casos es conveniente hacer una sustitución de variable para poder cumplir con el proceso de integración.

En general en una integral de la forma:

Teorema

Sea g una función cuyo rango es un intervalo I, y sea ƒ una función continua en I. Si g es derivable en su dominio y F es una antiderivada o primitiva de ƒ en I, entonces

Si u = g(x), entonces du = g’(x) dx, y

Ejemplos:

Calcular las siguientes integrales

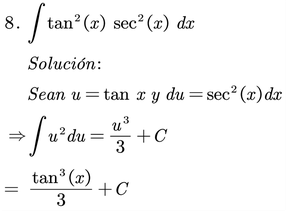
Verifica tu aprendizaje