El límite de una expresión del tipo k/0 puede ser +∞, -∞ o no tener límite.

Sea f la función definida por 

Y ahora veamos la siguiente tabla, en la que se muestra el comportamiento de f(x) cuando x se aproxima a 2 por la izquierda y por la derecha, que se denota:

Ejemplos:

Si le damos a la x un valor que se acerque a 1 por la izquierda como 0,999; el numerador es positivo y el denominador es negativo, por lo que el límite por la izquierda será: -∞.

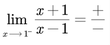
Como los límites laterales son diferentes, la función no tiene límite cuando x tiende a 1.

Definición

Definición

Ejemplo

Determinar el límite de cada función que se muestran a continuación, cuando x tiende a 1 por la izquierda y por la derecha.

Teorema

Si c es cualquier número real, y

Entonces se cumple:

Ejemplos:

Evaluar los siguientes límites

Verifica tu aprendizaje