De la misma manera en que se puede calcular por sustitución directa los límites de muchas funciones algebraicas, también las funciones trigonométricas fundamentales cuentan con esa propiedad, como se enuncia en el siguiente teorema.

Teorema: Límites de funciones trigonométricas

Dado θ un número real en el dominio de una función trigonométrica dada:

Además, dado un valor α, se cumple que:

Teorema

Si α es la medida de un ángulo dada en radianes, entonces podemos afirmar que:

Es importante recordar que la medida en radianes de un ángulo se define como:

Donde s es la longitud del arco que subtiende el ángulo, sobre una circunferencia de radio r, cuyo centro coincide con el vértice del ángulo.

Teorema. Dos límites trigonométricos especiales

Nótese que estos límites no pueden resolverse por ninguno de los métodos hasta ahora estudiados, y que su evaluación por sustitución directa nos genera una forma indeterminada.

Ejemplos:

Solución:

En este caso el ángulo de la función trigonométrica es 3x, por lo que para poder aplicar el teorema correspondiente necesitamos que también en el denominador el valor del argumento sea 3x. Para poder satisfacer este requerimiento multiplicamos por 3 tanto en el numerador como en el denominador.

Solución:

Solución:

La sustitución directa nos produce una forma indeterminada 0/0. Para ello utilizamos identidades trigonométricas para obtener una expresión equivalente tal como:

Solución:

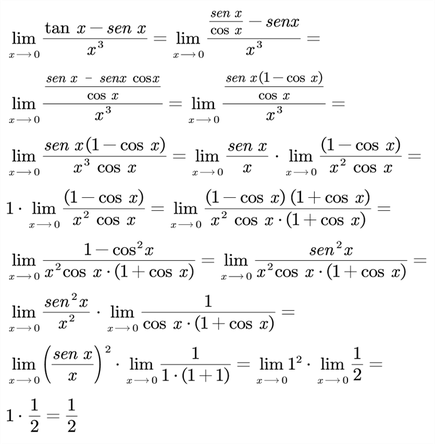
Solución:

Verifica tu aprendizaje