Límites y continuidad
El concepto de límite es la base fundamental con la que se construye el cálculo infinitesimal (diferencial e integral). Informalmente hablando se dice que el límite es el valor al que tiende una función cuando la variable independiente tiende a un número determinado o al infinito.
Idea intuitiva de límite
Iniciaremos nuestro estudio con la idea intuitiva de límite. Los ejemplos siguientes podrán mostrar una idea del significado del límite de una función en un punto.
Ejemplo:
Dada la función definida por:

Con dominio en el conjunto de los números reales, su representación gráfica es la siguiente:

Podemos ver el comportamiento de la función f para aquellos valores de x cercanos a 2 pero no iguales a 2.


Puede observarse de ambas tablas que conforme x se aproxima más a 2, f(x) toma, cada vez, valores más próximos a 3.
En otras palabras, al restringir el dominio de la función a valores cada vez "más cercanos a 2", el conjunto de imágenes o sea, los valores que toma la función, se "acercan cada vez más a tres".
En este caso se dice que cuando x tiende a 2, entonces f(x) tiende a 3.
Esto puede escribirse como:

Y utilizando notación de límites escribimos:

Que se lee: el límite de f(x) cuando x tiende a 2, es igual a 3.
Ejemplo:
Sea f la función definida por la ecuación:

La representación gráfica de f es:

En la gráfica puede observarse que aunque la función no está definida para x=2, cuando x toma valores muy cercanos a 2, la función se aproxima a 5, lo que escribimos como:

Generalización del concepto de límite
Sea f una función definida para valores reales en la cercanía de un número cualquiera b, aunque no necesariamente b mismo, tal como se representa en la gráfica:

Cuando x tiende a b, entonces f(x) tiende a L, lo que se escribe:

Definición de límite
Sea f una función definida en un intervalo abierto que contiene a b (excepto posiblemente en b) y L un número real cualquiera. La afirmación

Significa que

Propiedades de los límites
Hemos visto que el límite de f(x) cuando x se aproxima a b no depende necesariamente del valor de f en x = b, no obstante, puede darse el caso de que este límite sea f(b), caso, en el que se puede evaluar el límite directamente por sustitución.
Esto es:

Cuando el límite tiene este comportamiento, se dice que la función es continua en b.
Si b y k son números reales y n un número entero positivo, f y g son funciones con los límites siguientes:

Entonces:
Ley de la suma: El límite de una suma es igual a la suma de los límites:

Ley de la diferencia: El límite de una diferencia es igual a la diferencia de los límites:
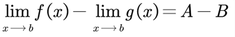
Ley del producto: El límite de un producto es igual al producto de los límites:

Ley del múltiplo constante: El límite del producto de una constante por una función es igual a la constante por el límite de la función:

Ley del cociente: El límite de un cociente es igual al cociente de los límites, siempre que el límite del denominador sea diferente de 0.

Si aplicamos la ley del producto repetidas veces con f ( x ) = g ( x ) , obtenemos la siguiente ley:
Ley de la potencia: Si n es un número entero positivo, entonces:

Ley de la función constante: El límite de una constante es igual a la constante misma:

Ley de la función identidad: El límite de la función identidad es igual al valor al cual "tiende" el límite:

Límites de funciones polinomiales y racionales
Si p es una función polinomial y b un número real, entonces:

Si r es función racional dada por r(x) = p(x)/q(x) y b un número real tal que al evaluar q en b su valor es distinto de cero, entonces:

Procedimiento para calcular límites
Ejemplos:


