Una función f derivable en un intervalo abierto I, es cóncava hacia arriba sobre I si f’ es creciente en el intervalo y cóncava hacia abajo en I si f’ es decreciente en ese intervalo.

La segunda derivada de una función f, también nos permite determinar extremos en un punto crítico.

Teorema.  Criterio de la segunda derivada para la concavidad de f

Sea ƒ una función cuya segunda derivada existe en un intervalo abierto I.

1. Si ƒ’’(x) > 0 para todo x en I, entonces la gráfica de ƒ es cóncava hacia arriba en I.

2. Si ƒ’’(x) < 0 para todo x en I, entonces la gráfica de ƒ es cóncava hacia abajo en I.

Ejemplos:

Determinar los intervalos abiertos en los que la gráfica de la siguiente función es cóncava hacia arriba o hacia abajo.

Puntos de inflexión

Sea f(x) una función dos veces derivable en el intervalo abierto I, entonces en I  hay un punto de inflexión cuando la función cambia su curvatura, es decir, cuando:

Punto de inflexión

En x=x_i tenemos un punto en el que cambia la curvatura de la función. Es por tanto un punto de inflexión. Si trazamos varias rectas tangentes a la curva de f, veremos que la recta tangente queda por encima de la curva de la función en un lado, y por debajo en otro. Además, el signo de la segunda derivada es diferente a la izquierda y a la derecha del punto, siendo f''(x_i)=0.

Teorema.  Punto de inflexión

Sea ƒ una función en un intervalo I. Si (c, f(c)) es un punto de inflexión de la curva f, entonces f’’(c)=0 o no existe la segunda derivada de f en el punto x=c.

Ejemplo:

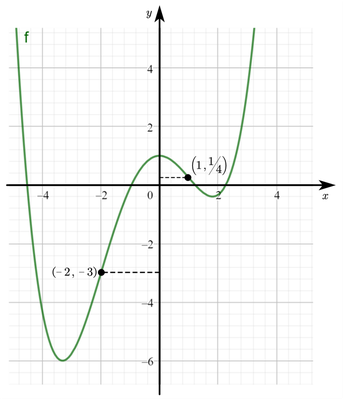
Determinar los puntos de inflexión de la función dada por la siguiente ecuación:

Los puntos (-2, -3) y (1, ¼) son los puntos en los que se da el cambio de concavidad y por lo tanto son puntos de inflexión.

El criterio de la segunda derivada además de servir para analizar la concavidad, también permite determinar los máximos y mínimos relativos de la función. Ello se fundamenta en el hecho de que una función cóncava hacia arriba en un intervalo abierto y que contiene a x y f’(x)=0, entonces f(x) es un mínimo relativo de f. De igual forma, si la gráfica de f es cóncava hacia abajo en un intervalo abierto que contiene a x y f’(x)=0, entonces f(x) es un máximo relativo de f.

Teorema.  Criterio de la segunda derivada para máximos y mínimos de f

Sea ƒ una función tal que f’(c) = 0 y la segunda derivada existe en un intervalo abierto I que contiene a x.

1.       Si ƒ’’(x) > 0 para todo x en I, entonces la gráfica de ƒ tiene un mínimo relativo en (x, f(x)).

2.       Si ƒ’’(x) < 0 para todo x en I, entonces la gráfica de ƒ tiene un máximo relativo en (x, f(x)).

Si f’’(x) = 0, podría ser que f tenga un mínimo relativo, un máximo relativo o ninguno de ellos. En tal caso prevalece el criterio de la primera derivada.

Ejemplo:

Determinar los puntos críticos y puntos de inflexión de la función dada por la siguiente ecuación:

Verifica tu aprendizaje

Para cada una de las siguientes funciones, determinar los puntos críticos, los intervalos de variación y concavidad de la función. Grafique la función.