Consideremos la función f(x) = x² con dominio real y cuya gráfica adjuntamos. Podemos observar en ella que conforme x crece hacia el infinito, f(x) tiende sin límite al infinito, de igual forma si x toma valores cada vez menores negativamente, f(x) aumenta sin límite positivamente.

Enunciamos entonces el siguiente teorema.

Sea n un entero positivo, entonces:

Límites al infinito

Analizaremos a continuación aquellos límites en los que no solo f(x) aumenta o disminuye, sino cuando la variable x tiende al infinito, sea positivo o negativo.

Consideremos la función f(x) = 1/x con dominio en el conjunto de los números reales menos 0 y cuya gráfica se muestra a continuación.

Podemos observar que cuando x toma valores mayores positivamente sin límite f(x) tiende cada vez más a cero, acercándose al eje X .  De igual forma si x toma valores menores sin límite hacia el infinito negativo, la gráfica de f(x), también tiende a 0.

Teorema.

Si k es una constante y n es un número racional positivo, entonces

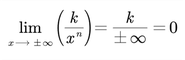
Reglas algebraicas relativas a ±∞

Siendo k un número entero real, se satisfacen las siguientes propiedades algebraicas

Las leyes sobre límites finitos son válidas para los límites infinitos.  Si al evaluar límites infinitos llegamos a expresiones como:

Entonces consideramos esa expresión como una expresión indefinida.

Se resumen a continuación las reglas algebraicas para los límites infinitos

Ejemplos:

Para límites de  funciones racionales que tienden a ±∞, se cumple que:

Verifica tu aprendizaje

Evaluar los siguientes límites