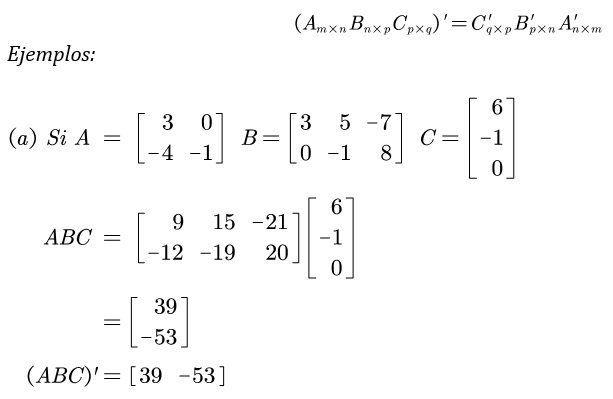Tipos especiales de matrices

En esta sección se estudiarán tres tipos especiales de matrices: las matrices diagonales, las matrices identidad y las matrices nulas.

Matrices diagonales

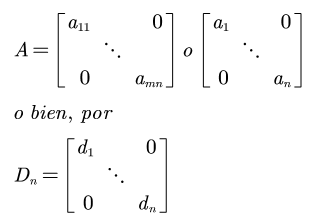
Una matriz diagonal es una matriz cuadrada cuyos elementos son todos iguales a cero, excepto los que pertenecen a su diagonal principal, la cual es la que va del extremo superior izquierdo al extremo inferior derecho; así pues,

(cuando todos los elementos de una matriz son ceros, se trata de una matriz nula, la cual se describirá más adelante)

Una matriz diagonal n x n puede indicarse por la notación

Ejemplos:

Matriz identidad

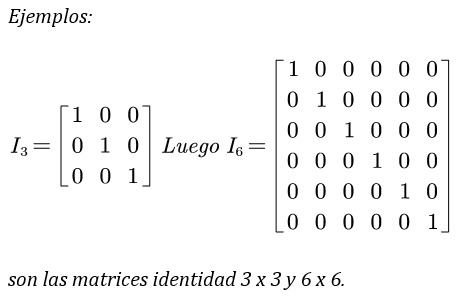
Una matriz identidad es una matriz diagonal cuyos elementos de la diagonal principal son todos iguales al número uno. Por consiguiente,

o en forma equivalente, una matriz diagonal Dn es una matriz identidad si y sólo si

Una matriz identidad n x n se representa por In.

Nótese que al premultiplicar o posmultiplicar una matriz por la matriz identidad del tamaño (u orden) apropiado, no cambia la matriz dada; es decir,

Matriz nula

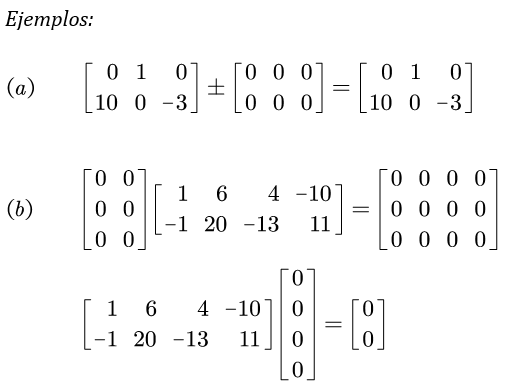
Una matriz nula es una matriz m x n cuyos elementos son todos iguales a cero; se simboliza con O. Cuando una matriz nula del orden (o tamaño) apropiado se suma o se resta de otra matriz, esta última no cambia; es decir,

Premultiplicar o posmultiplicar una matriz nula de orden apropiado da lugar a otra matriz nula;

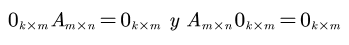
Transpuesta de una matriz

En muchos análisis en los que intervienen matrices, es conveniente emplear la transpuesta de una matriz. En esta sección se define la transpuesta de una matriz, le dé una suma o diferencia de matrices, y la de un producto de matrices.

La transpuesta de una matriz A de orden m x n es una matriz de orden n x m, denotada por A´, cuyas filas son las columnas de A, y cuyas columnas son las filas de A. Por tanto, si…

Entonces la transpuesta de A es

Nótese que la transpuesta de un vector fila n-dimensional es un vector columna también n-dimensional, y análogamente, la transpuesta de un vector columna de n-dimensiones es un vector fila de n-dimensiones también. La transpuesta de una matriz diagonal es la misma matriz diagonal.

Si una matriz (cuadrada) y su transpuesta son iguales, es decir, ai j =a j i para toda i y toda j, entonces la matriz se denomina simétrica (con respecto a su diagonal principal).

Una matriz simétrica que al multiplicarse por sí misma queda igual, se dice que es idempotente. Por tanto, A es idempotente si y sólo si

Transpuesta de una suma o de una diferencia de matrices

La transpuesta de una suma o diferencia de matrices es igual a la suma o diferencia de las transpuestas de las matrices; por consiguiente,

Transpuesta de un producto de matrices

La transpuesta de un producto de matrices es igual al producto de las transpuestas de las matrices tomadas en orden inverso; por tanto,