Inversa de una matriz

En la teoría de matrices solamente ciertas clases de matrices cuadradas tienen inverso multiplicativos a diferencia de álgebra común donde cada número real a diferente de cero tiene su inverso multiplicativo b.

Matriz adjunta

Definición: Si A es una matriz cuadrada n x n y B es la matriz de sus cofactores, entonces la Adjunta de A, denotada por adjA que es la transpuesta de la matriz B cuadrada n x n.

Inversa de una matriz

Si A es una matriz cuadrada de orden n. Si existe una matriz B tal que

AB = In = BA

entonces B se llama inversa de A y se denota con A-1. (Se lee “A inversa”)

Si A es una matriz cuadrada tiene una inversa y decimos que A es invertible. Si A no es una matriz cuadrada no es posible invertirla.

Ejemplo:

Inversa de una matriz 2 x 2

Método I:

TEOREMA:

Si el determinante de A no es cero el inverso multiplicativo de A es:

Ejemplo:

Obtener la matriz inversa de A.

Solución:

1. Calcular el determinante de A

     |A|=12-5=7

2. Se calcula la Adj(A)

3. Formamos la matriz B y obtenemos la transpuesta de B que es su adjunta

4. Aplicamos el teorema

5. Comprobamos que:

Ejemplo:

Solución:

Calculamos el determinante de A

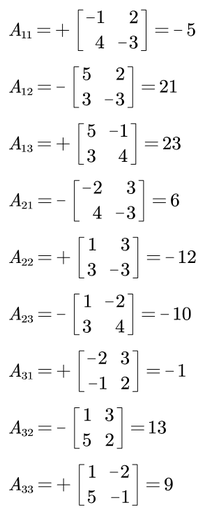
Calculamos todos los cofactores

3. Formamos la matriz B y su transpuesta

4. Generamos la inversa de A