Espacios vectoriales
Un espacio vectorial V (o espacio lineal) sobre R es un conjunto de objetos sobre los cuales se ha definido una suma, denotada con el símbolo ”+” y un producto escalar (una manera de multiplicar estos objetos con números reales) denotado de la manera usual y que cumple las siguientes propiedades:

Vectores en el espacio

Un sistema de coordenadas tridimensional se construye trazando un eje Z, perpendicular en el origen de coordenadas a los ejes X e Y.
Cada punto viene determinado por tres coordenadas P(x, y, z).
Los ejes de coordenadas determinan tres planos coordenados: XY, XZ e YZ. Estos planos coordenados dividen al espacio en ocho regiones llamadas octantes, en el primer octante las tres coordenadas son positivas.
Un vector en el espacio es cualquier segmento orientado que tiene su origen en un punto y su extremo en el otro.
Componentes de un vector en el espacio
Si las coordenadas de A y B son: A(x1, y1, z1) y B(x2, y2, z2). Las coordenadas o componentes del vector AB son las coordenadas del extremo menos las coordenadas del origen.

Ejemplo:
Determinar la componente de los vectores que se pueden trazar en el triángulo de vértices: A(-3,4,0), B(3,6,3) y C(-1,2,1).

Módulo de un vector
El módulo de un vector es la longitud del segmento orientado que lo define. El módulo de un vector es un número siempre positivo y solamente el vector nulo tiene módulo cero.
Cálculo del módulo conociendo sus componentes
Si conocemos los componentes de un vector, entonces se tiene que:

Ejemplo: Dados los vectores

Hallar los módulos de cada uno de ellos.
Solución:

Cálculo del módulo conociendo las coordenadas de los puntos
La distancia entre dos puntos es igual al módulo del vector que tiene de extremos dichos puntos.

Ejemplo: Hallar la distancia entre los puntos A(1, 2, 3) y B(−1, 2, 0).

Vector unitario
Un vector unitario tiene de módulo la unidad.
La normalización de un vector consiste en asociarle otro vector unitario, de la misma dirección y sentido que el vector dado, dividiendo cada componente del vector por su módulo.

Operaciones con vectores en el espacio
Suma de vectores
Para sumar dos vectores se suman sus respectivas componentes.

Ejemplos:
Dados los vectores:

Solución:

Dados los vectores:

Dependencia e independencia lineal
Combinación lineal
Una combinación lineal de dos o más vectores es el vector que se obtiene al sumar esos vectores multiplicados por sus correspondientes escalares.


Cualquier vector se puede poner como combinación lineal de otros que tengan distinta dirección.

Esta combinación lineal es única.
Vectores linealmente dependientes
Varios vectores libres del plano se dice que son linealmente dependientes si hay una combinación lineal de ellos que es igual al vector cero, sin que sean cero todos los coeficientes de la combinación lineal.

Propiedades
- Si varios vectores son linealmente dependientes, entonces al menos uno de ellos se puede expresar como combinación lineal de los demás.

También se cumple el reciproco: si un vector es combinación lineal de otros, entonces todos los vectores son linealmente dependientes.
2. Dos vectores del plano son linealmente dependientes si, y sólo si, son paralelos
3. Dos vectores libres del plano

Son linealmente dependientes si sus componentes son proporcionales.

Ejemplo:
Determinar los valores de k para que sean linealmente dependientes los vectores:

Los vectores son linealmente dependientes si el determinante de la matriz que forman es nulo, es decir que el rango de la matriz es menor que 3.

Vectores linealmente independientes
Varios vectores libres son linealmente independientes si ninguno de ellos puede ser escrito con una combinación lineal de los restantes.

Los vectores linealmente independientes tienen distinta dirección y sus componentes no son proporcionales.

Ejemplos:
1. Determinar si son linealmente dependientes o independientes los vectores

Sistema incompatible indeterminado (Th. De Rouché)
El sistema tiene infinitas soluciones, por tanto, los vectores son linealmente dependientes.
Base
Dados tres vectores cualesquiera

Con distinta dirección forman una base, porque cualquier vector del espacio se puede poner como combinación lineal de ellos.

Las coordenadas del vector respecto a la base son:

Base ortogonal
Una base es ortogonal si los vectores de la base son perpendiculares entre sí.
Base ortonormal
Una base es ortonormal si los vectores de la base son perpendiculares entre sí, y además tienen módulo 1.

Esta base formada por los vectores i, j y k se denomina base canónica.
Ejemplo:
Para que valores de a los vectores

Forman una base.

Producto escalar
El producto escalar de dos vectores es un número real que resulta al multiplicar el producto de sus módulos por el coseno del ángulo que forman.

Expresión analítica del producto escalar

Ejemplo:
Hallar el producto escalar de dos vectores cuyas coordenadas en una base ortonormal son:
(1, 1/2, 3) y (4,−4, 1).
Solución:
(1, 1/2, 3) · (4, −4, 1) = 1 · 4 + (1/2) · (−4) + 3 · 1 = 4 −2 + 3 = 5
Expresión analítica del módulo de un vector

Hallar el valor del módulo de un vector de coordenadas u= (−3, 2, 5) en una base ortonormal.

Vectores ortogonales
Dos vectores son ortogonales si su producto escalar es 0.

Ejemplo:
Calcular los valores x e y para que el vector (x, y,1) sea ortogonal a los vectores (3, 2, 0) y (2, 1,−1).

El producto escalar de un vector no nulo por sí mismo siempre es positivo.

Ejemplos:
Dados los vectores:


Producto vectorial
El producto vectorial de dos vectores es otro vector cuya dirección es perpendicular a los dos vectores y su sentido sería igual al avance de un sacacorchos al girar de u a v. Su módulo es igual a:
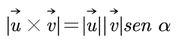
El producto vectorial se puede expresar mediante un determinante:

Ejemplos:
1. Calcular el producto vectorial de los vectores u= (1, 2, 3) y v= (−1, 1, 2).

2. Dados los vectores

Hallar el producto vectorial y comprobar si el vector encontrado es ortogonal a los vectores generadores.

Producto mixto
El producto mixto de tres vectores cualesquiera, es igual al producto escalar del primer vector por el producto vectorial de los otros dos.
El producto mixto se representa por:

El producto mixto de tres vectores es igual al determinante que tiene por filas las coordenadas de dichos vectores respecto a una base ortonormal.

Ejemplos
Calcular el producto mixto de los vectores:



