Determinantes
Los determinantes los obtenemos de las matrices mediante simples operaciones aritméticas.
Recuerda que llamamos dimensión de una matriz al número de filas y columnas que tiene (m x n) y si la matriz es cuadrada tendrá el mismo número de filas que de columnas y la representamos por (n x n).
Si n vale 1 hablamos de matrices orden 1, si n vale dos serán matrices de orden 2, si n vale 3 serán de orden 3, y así sucesivamente. Lo mismo cabe decir para los determinantes.
¿Cómo se escriben los determinantes?
Casi igual que las matrices, en lugar de utilizar grandes paréntesis como:

Los elementos en los determinantes se colocan entre dos rayas verticales y el nombre también:

¿Cómo escribimos un determinante de orden 1?
Dado que solo tiene una fila y una columna no es más que un número:

¿Cómo escribimos un determinante de orden 2?
Como tiene dos filas y dos columnas escribiremos:

¿Cómo calculamos el valor de un determinante de orden 2?
Es una simple resta de números: producto de los elementos de la diagonal principal menos el producto de los elementos de la diagonal secundaria:
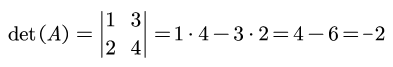
Ejemplos:
Calcular el valor de los siguientes determinantes

¿Cómo calculamos el valor de un determinante de orden 3?
Un modo sería aplicando la regla de Sarrus (Pierre Frédéric Sarrus, Saint-Affrique, 10 de marzo de 1798 - 20 de noviembre de 1861) fue un matemático francés. En 1815, Sarrus dudaba entre escoger Medicina o Matemáticas para continuar su carrera. El rechazo del alcalde de Saint-Affrique de otorgarle un certificado de buena vida y costumbres a causa de sus opiniones bonapartistas y de sus orígenes protestantes le obligan a optar por la facultad de Ciencias) que consiste en multiplicar los elementos en el orden que se señalan en la figura siguiente y que después vamos a resolver por este método:

Multiplicamos los elementos de las diagonales principales y vamos sumando los productos obtenidos:

Hallamos la diferencia de las dos cantidades obtenidas y será el valor del determinante:


Propiedades de los determinantes
1) Un determinante es nulo si tiene:
a.- Dos filas iguales

b.- Dos columnas iguales

c.- Si todos los elementos de una fila o columna son ceros

d.- Si los elementos de una fila o columna proceden del producto o cociente de un número por los elementos de otra fila o columna el valor del determinante es 0

La columna 3 es resultado de multiplicar la 1 por el factor 4
2) El valor de un determinante triangular es igual al producto de la diagonal principal

3) El valor del determinante de una matriz y el de su transpuesta es el mismo

4) En un determinante, si se cambian dos líneas paralelas (filas o columnas) el determinante cambia de signo

Ejemplos:
a) Sin realizar operaciones, cuál es el valor de:

Respuesta: det(M) = 10
Justificación: Se trata de un determinante triangular superior y la respuesta viene dada por el producto de los elementos de la diagonal principal.
b) Sin realizar operaciones, cuál es el valor de:

Respuesta: det(Z) = 0
Justificación: Se trata de un determinante en el que la 1ª y 3ª columnas son iguales.
5) Si multiplicas a todos los elementos de una fila o columna por un número, el determinante queda multiplicado por este número:

6) El determinante del producto de dos matrices cuadradas y del mismo orden es igual al producto de sus determinantes
Tenemos las matrices:

7) A los elementos de una fila o columna puedes descomponerlos en dos sumandos. Con los sumandos obtenidos escribes dos determinantes (con cada uno de estos sumandos) permaneciendo los mismos elementos de las otras dos líneas que los repites en cada determinante.
La suma de dos determinantes equivale al determinante primitivo.
Dado el determinante:

Vamos a descomponer los elementos de la tercera fila en dos sumandos

Ejemplos:
a) Obtenga el valor del determinante

Sin realizar cálculos inferimos que el resultado de ese determinante es 0.
Solución
La fila 4ª es linealmente dependiente de la 1ª (Ha sido multiplicada por 2).
b) Si a los elementos de una fila de un determinante de orden 3 cuyo valor es 24 los multiplico por 3
¿qué valor adquiere el nuevo determinante?
Respuesta: 72 (24 X 3)
