Álgebra Lineal
Matrices
En muchos análisis se supone que las variables que intervienen están relacionadas mediante un conjunto de ecuaciones lineales. El álgebra matricial proporciona una notación concisa y clara para la formulación y resolución de tales problemas, muchos de los cuales serían casi imposibles de plantear con la notación algebraica ordinaria.
¿Qué es una matriz?
Es algo muy simple, se trata de un conjunto de elementos (casi siempre números) debidamente colocados en filas y columnas.
Ejemplo:

Esta matriz consta de 20 números colocados en filas y columnas.
El número de filas es 5 y el de columnas 4.
Se puede comprobar que número de filas por número de columnas es igual al total de elementos (o dimensión de la matriz).
Para buscar un elemento indicamos primero la fila donde se encuentra y seguidamente la columna:
El número -12 se halla en el lugar (5,2) ó (5 2)
El número 15 se halla en el lugar (4,3) ó (4 3)
¿Tiene alguna utilidad escribir datos en forma de filas y columnas, es decir, en forma de matriz?
Las matrices las encontramos en la vida de cada día, en la información periodística, en tablas de información, etc.
Ejemplo:
Países más afectados por pandemia del Sars-Cov2, año 2020
La tabla anterior es una matriz. En esa tabla o matriz puedes encontrar con facilidad la situación de los 10 países más afectados al 13 de junio de 2020 por el virus Sars-Cov2, así como afectados, fallecidos y curados por ejemplo.
¿Para qué sirven las matrices?
Esta pregunta nos la planteamos puesto que no vamos a estudiar MATRICES, simplemente para hacer unas tablas como la que hemos visto antes. Sirven para otras cosas también, especialmente, para resolver ecuaciones de primer grado con muchas incógnitas.
Escribir una matriz
Como podríamos tener varias matrices, lo normal será dar nombre a cada una de ellas. Basta con designarla con una letra mayúscula.
Los elementos que contiene una matriz conviene escribirlos entre paréntesis, de la siguiente forma:

Cada elemento, en este caso cada valor numérico ocupa un lugar determinado teniendo en cuenta su fila y columna, en este orden:
El 2 ocupa el número 1 de fila y 1 de columna, (1,1).
El 6 ocupa el número 2 de fila y 3 de columna, (2,3).
El – 2 ocupa el número 3 de fila y 1 de columna, (3,1).
Primero se tiene en cuenta el número de fila y en segundo lugar el de la columna.
Aplicaciones que suelen utilizar matrices, por ejemplo: cuando has de resolver ecuaciones de primer grado con varias incógnitas:
Un sistema de ecuaciones de primer grado podría ser:

Tomando los coeficientes (con sus signos) de las incógnitas podemos escribir la siguiente matriz:

Con los términos independientes (los que se encuentren a la derecha del signo igual), podemos escribir la siguiente matriz:

Definición de Matriz
Una matriz es una disposición (o “arreglo”) rectangular de números en la forma

Las letras ai j representan números reales, que son los elementos de la matriz. Nótese que ai j designa al elemento en la i-ésima fila y la j-ésima columna de la matriz A; la matriz A se denota también a veces por (ai j) o por {ai j}. Una matriz que tiene m filas y n columnas se dice que es una matriz m x n (“m por n”), o bien, una matriz de orden m x n. Si m = n, se expresa que la matriz es cuadrada. Cuando han de realizarse varias operaciones en matrices, su orden suele denotarse mediante subíndices, por ejemplo:


Se dice que dos matrices del mismo orden son iguales solamente si todos sus elementos correspondientes son también iguales, es decir, si las matrices son idénticas. Observemos que, por definición, las matrices que son de diferente orden no pueden ser iguales.
Ejemplo:
Si se tienen las siguientes matrices:

Definición de Vector
Una matriz que consta de una sola columna, es decir, una matriz m x l se conoce como vector columna, y se expresa como
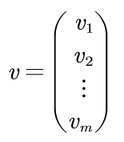
Las letras vi son números reales: los componentes del vector; vi es el i-ésimo componente del vector v. Un vector columna que tiene m filas se dice que es un vector de m componentes, o que es m-dimensional.
Análogamente, una matriz que contiene una sola fila, es decir, una matriz 1 x n, se dice que es un vector fila y se expresa como

Las letras vj son números reales: los componentes del vector; vj es el j-ésimo componente del vector v. Un vector fila con n columnas se dice que es un vector de n componentes, o que es n-dimensional.

Dos vectores fila que tienen el mismo número de columnas, o dos vectores columna que tienen el mismo número de filas, se dice que son iguales solamente si todos los elementos correspondientes son también iguales, es decir, si los vectores son idénticos.
Ejemplos:
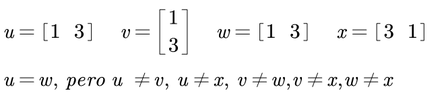
NOTA: Con frecuencia es útil considerar a una matriz como compuesta de una serie de vectores fila o de vectores columna; por ejemplo, la matriz

O bien compuesta por tres vectores fila:


