Polígonos

 

 

 

Definición:  Un polígono es una porción del plano limitada por segmentos de recta consecutivos no alineados.

 

 

Un polígono se denomina convexo si todos sus ángulos internos son estrictamente menores de 180 grados y todas sus diagonales son interiores.

 

 

Un polígono es cóncavo si al menos uno de sus ángulos internos es mayor que 180°.

De las imágenes anteriores, puedes observar que los ángulos internos del polígono son los formados por dos lados consecutivos y los ángulos externos son los ángulos adyacentes a cada ángulo interno, como resultado de prolongar los lados siempre en un mismo sentido.

 

Clasificación de los polígonos
Los polígonos se clasifican por sus lados como polígonos regulares y polígonos irregulares.

Polígonos regulares: Son aquellos que tienen todos sus lados y ángulos iguales.
Polígonos irregulares:  Las medidas de sus lados y ángulos son diferentes.

De acuerdo con el número de lados los polígonos reciben diferentes nombres, así tenemos que:

 

Número de lados

Nombre

Número de lados

Nombre

3

Triángulo

12

Dodecágono

4

Cuadrilátero

13

Tridecágonmo

5

Pentágono

14

Tetradecágono

6

Hexágono

15

Pentadecágono

7

Heptágono

16

Hexadecágono

8

Octágono

17

Heptadecágono

9

Nonágono

18

Octadecágono

10

Decágono

19

Nonadecágono

11

Undecágono

20

Icoságono

 

Elementos de un polígono
Vértice:  Es el punto donde concurren dos lados consecutivos.
Ángulo interior:  Como ya se enunció es el ángulo formado por dos lados adyacentes.
Ángulo exterior: El que se forma con la prolongación de los lados en un mismo sentido y su lado adyacente.
Centro: El centro de un polígono regular es el centro de la circunferencia circunscrita al polígono.
Radio: Es el segmento que une el centro del polígono con un vértice, corresponde al radio de la circunferencia circunscrita.

Apotema: Segmento perpendicular a cualquiera de los lados del polígono desde el centro del polígono.
Ángulo central: Es el ángulo formado por dos radios, correspondientes a dos vértices consecutivos.
Diagonal: Es el segmento de recta que une dos vértices no adyacentes.
Número de diagonales de un polígono
El número de diagonales de un polígono está en función del número de lados del polígono. Desde cada vértice del polígono se pueden trazar (n – 3) diagonales, donde n es el número de lados del polígono.  Por lo tanto, el número total de diagonales está dado por la fórmula:

Donde n es el número de lados del polígono.

 

Ejemplos:

1. Calcular y trazar el número total de diagonales de un pentágono.

 Solución:

\[\begin{align*} D &= \frac{n(n-3)}{2} \\ D &= \frac{5(5-3)}{2} \\ D &= \frac{10}{2} \\ D &= 5 \end{align*}\]

2. Calcular y trazar el número total de diagonales de un octágono.

 Solución:

 

\[\begin{align*} D &= \frac{n(n-3)}{2} \\ D &= \frac{8(8-3)}{2} \\ D &= \frac{40}{2} \\ D &= 20 \end{align*}\]

3. ¿En cuál polígono, se pueden trazar en total 152 diagonales?
Solución:

\[\begin{align*} D &= \frac{n(n-3)}{2} \\ 152 &= \frac{n(n-3)}{2} \\ 152 \cdot 2 &= n^{2}-3n \\ n^{2} -3n -304 = 0 \\ (n-19)(n+16)&=0 \\ n_{1} = 19\ &y\ n_{2} = -16 \end{align*}\]

 R./ El polígono en el cual se pueden trazar 152 diagonales es un nonadecágono.

 

Ejercicios:
1. Determinar el número total de diagonales de un:
a. Hexágono
b. Heptágono
c. Undecágono
d. Octadecágono
e. Icoságono

 

2. ¿En cuál polígono es posible trazar 17 diagonales desde 1 vértice?

 

3. ¿En cuál polígono es posible trazar 9 diagonales desde 1 vértice?

 

4. ¿En cuál polígono es posible trazar 6 diagonales desde 1 vértice?

 

5. Traza un hexágono en una circunferencia, puedes trabajar con geogebra o con lápiz y compás. (Para trazar un hexágono en una circunferencia, te das un punto cualquiera en la circunferencia y a partir de ahí vas trazando seis circunferencias de igual radio a la circunferencia original). Observa que en lugar de las diagonales tenemos arcos de circunferencia uniendo los vértices no adyacentes. Colorea la imagen.


 

Ángulos de un polígono

Las medidas de los ángulos de un polígono, se obtienen con las siguientes fórmulas:

 

Suma de los ángulos internos

La suma de los ángulos internos de cualquier polígono se obtiene con la fórmula

Donde n es el número de lados del polígono.

  

Suma de los ángulos externos

La suma de los ángulos externos de cualquier polígono es 360°.

 

Medida de los ángulos internos de cualquier polígono regular

En un polígono regular obtenemos la medida de cualquier ángulo interno de la siguiente forma:

Donde n es el número de lados del polígono.

 

Medida de los ángulos externos de cualquier polígono regular

En un polígono regular obtenemos la medida de cualquier ángulo externo de la siguiente forma:

Donde n es el número de lados del polígono.


Ejemplos:
1. ¿Cuál es el polígono regular que tiene un ángulo exterior de 120°?
Solución:

R./ El polígono es un triángulo equilátero.


2. Cinco ángulos internos de un hexágono miden: 120°, 75°, 140°, 85° y 60°. ¿Cuánto mide el sexto ángulo y que tipo de polígono es?
Solución:

 R./ El sexto ángulo mide 240° y el polígono es cóncavo irregular.

 

3. En un polígono regular la sumatoria de sus ángulos internos es 2340°. ¿Cuál es ese polígono?
Solución:

\[\begin{align*} S_{i} &= 180°(n-2) \\ 2340° &= 180°(n-2) \\ 2340° &= 180°n - 360° \\ 2340° + 360° &= 180°n \\ 2700° &= 180°n \\ \therefore n &= \frac{2700°}{180°} \\ n &= 15 \end{align*}\]

R./ Ese polígono es un pentadecágono.

 

4. ¿Cuántos lados tiene un polígono regular y uno de sus ángulos internos mide 144°?
Solución:

\[\begin{align*} i &= \frac{180°(n-2)}{n} \\ 144° &= \frac{180°n - 360°}{n} \\ 144° n &= 180°n - 360° \\ 144°n - 180°n &= -360° \\ -36n &= 360°n \\ \therefore n &= \frac{-360°}{-36°} \\ n &= 10 \end{align*}\]

R./ El polígono es un decágono ya que tiene 10 lados.


Ejercicios:
1. Determine la suma de los ángulos internos de los siguientes polígonos:
a. Rombo
b. Pentágono
c. Nonágono
d. Undecágono
e. Tetradecágono
f. Un polígono de 35 lados


2. Determine la media de los ángulos internos de los siguientes polígonos:
a. Hexágono
b. Heptágono
c. Octágono
d. Dodecágono
e. Pentadecágono
f. Icoságono


3. ¿En cuál polígono la suma de los ángulos internos es 1260°?


4. ¿En cuál polígono la suma de los ángulos internos es 1620°?


5. ¿En cuál polígono la suma de los ángulos internos es 2520°?


6. ¿Cuál es el polígono regular cuyos ángulos internos miden 157,5° cada uno?


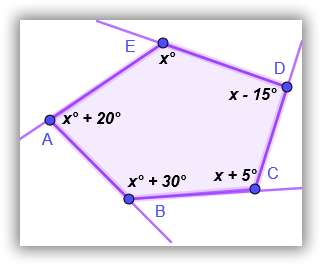
7. Determine el valor de cada uno de los ángulos internos y externos del siguiente polígono.

 

Siguiente tema: Áreas de polígonos