Integración por fracciones parciales
Definición: Una función racional de la forma P(x)/Q(x) es una Fracción propia, si el grado del polinomio P(x) es menor que el grado del polinomio Q(x).
Si al contrario el grado del polinomio P(x) es mayor o igual al polinomio Q(x), la fracción se denomina Fracción impropia. Toda fracción impropia se puede expresar como la suma de un polinomio más una fracción propia. Es decir:

El método de fracciones parciales permite resolver integrales de funciones racionales que no se pueden resolver por otros métodos.
Fracciones propias
En el caso de las fracciones propias el denominador debe factorizarse completamente, en factores de cualquiera de las siguientes formas:

Factores lineales
Para factores lineales de la forma (ax + b)n (donde n es un número natural), la descomposición en n fracciones parciales debe seguir el siguiente modelo:

Ejemplos: Descomponer en fracciones parciales e integrar







Factores cuadráticos
Para cada factor de la forma (ax2+bx+c)n, siendo n un número natural y el discriminante de ax2+bx+c menor que cero. La descomposición en fracciones parciales debe incluir la suma de las siguientes n fracciones.
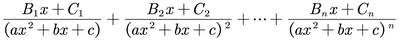
Donde B1,….,Bn, C1,….,Cn son constantes a determinar.
Ejemplos: Descomponer en fracciones parciales e integrar



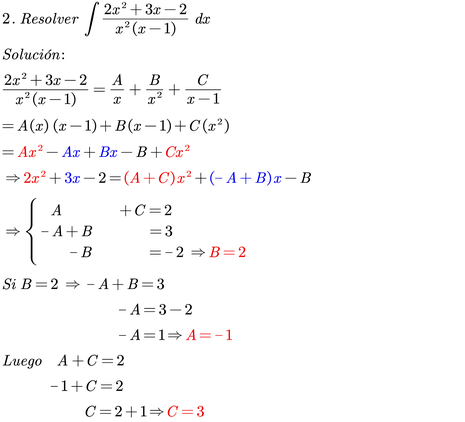

Fracciones impropias
Si la fracción es impropia, es decir, el grado del numerador es mayor o igual que el grado del denominador; se debe dividir el denominador entre el numerador para obtener:

Aplicando las propiedades de las integrales, se descompone la integral en la suma de dos integrales:

Ejemplos: Descomponer en fracciones parciales e integrar



Verifica tu aprendizaje
Resuelva las integrales usando fracciones parciales


